Algorithmen
Computer lösen viele Probleme durch die enorm schnelle automatische Verarbeitung von Daten. Das genaue Vorgehen wird durch Algorithmen festgelegt.
Der Computer arbeitet ausschliesslich mit digitalisierten Daten. Doch was genau er damit machen soll, muss man ihm sagen, mit sogenannten Algorithmen.
Algorithmus
Ein Algorithmus ist eine eindeutige Handlungsanweisung für die Lösung von Problemen. Algorithmen bestehen aus endlich vielen, wohldefinierten Einzelschritten. Sie können in menschlicher Sprache formuliert oder aber zur Ausführung in ein Computerprogramm implementiert werden. Für die Problemlösung wird eine bestimmte Eingabe Schritt für Schritt in eine bestimmte Ausgabe überführt.
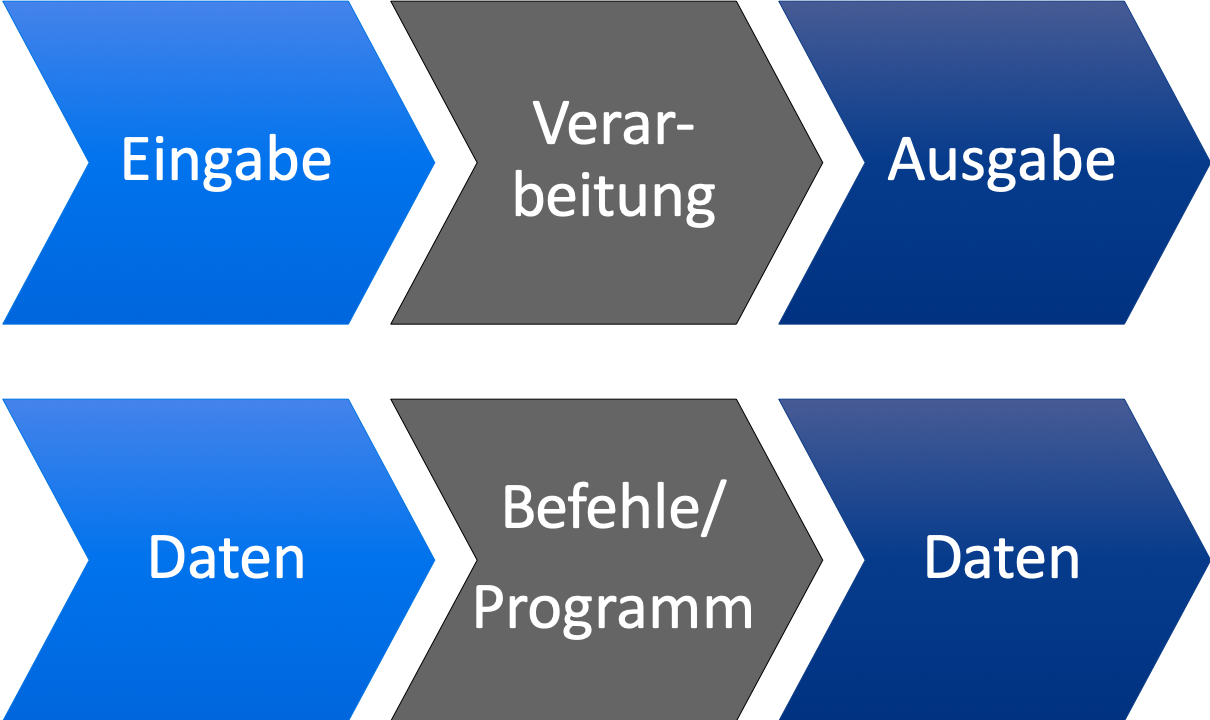
Auch Algorithmen folgen dem EVA-Prinzip:
EVA
EVA: Eine Eingabe wird mittels automatischer Verarbeitung in eine Ausgabe verwandelt.
Beispiele:
- Sie schalten den Computer an (= Eingabe) – es dauert ein Weilchen, bis er gebootet hat (= Verarbeitung): Sie sehen die Oberfläche des Betriebssystems (= Ausgabe).
- Sie klicken auf das Firefox-Icon (das ist die Eingabe) – das Programm wird in den Arbeitsspeicher geladen (= Verarbeitung): Sie sehen das Browserfenster am Bildschirm (= Ausgabe).
- Sie schreiben www.oinf.ch in die Adressleiste des Browsers und drücken Return (E) – die Webseite wird aus dem Internet geholt und in einem temporären Cache lokal gespeichert (V): Die Seite wird im Browserfenster angezeigt (A).
- Sie tippen 5+17 in ein Rechenprogramm (E) – die Rechnung wird ausgeführt (V): Das Ergebnis 22 wird angezeigt oder abgespeichert (A).
- Sie schreiben
move();in die act-Methode einer Actor-Klasse im Greenfoot Editor und lassen das Szenario laufen (E) – der Code wird kompiliert und ausgeführt (V): Das Bild der Actor-Instanz bewegt sich um 10 Pixel geradeaus (A).
Analogie
Getränkeautomat: Münzen einwerfen und Wahltasten drücken (E) – Es passiert was mit Strom und Zahnrädern (V) – Getränk und ggf. Wechselgeld werden ausgegeben (A).
Die Analogie zeigt einen der wichtigen Vorteile des EVA-Prinzips: Eine EVA-Maschine kann man benutzen, ohne dass man verstehen müsste, wie genau die Verarbeitung vor sich geht.
Anforderungen
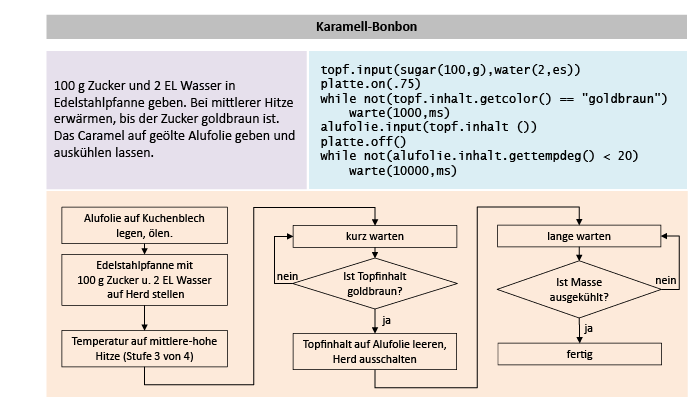
Ein Algorithmus ist also ein Lösungsweg, eine Verarbeitungsvorschrift, die so präzise formuliert ist, dass selbst ein Automat (bzw. Computer) durch die sture Befolgung der Anweisungen zur Lösung kommt – in etwa so, wie man auch als unfähiger Koch zu einem guten Kuchen kommen kann, indem man stur das Rezept befolgt.
Genau genommen muss ein solcher Lösungsweg noch ein paar Anforderungen erfüllen, damit er wirklich als Algorithmus gelten kann:
Anforderung 1: Allgemeinheit
Allgemeinheit bedeutet, dass nicht nur ein einzelnes Problem, sondern eine ganze Klasse von Problemen gelöst werden soll. Nur weil man weiss, dass 7 + 4 elf ergibt, kann man noch nicht addieren. Erst wer alle möglichen Zahlen addieren kann, hat die Addition allgemein begriffen.
Anforderung 2: Eindeutigkeit
Eindeutigkeit bedeutet, dass die Abfolge der einzelnen Schritte genau festgelegt ist. Zwar gibt es mit Verzweigungen und Schleifen die Möglichkeit, (potentielle) Änderungen dieser Reihenfolge einzubauen, aber wann das passiert, ist ebenfalls eindeutig festgelegt. Die Möglichkeit, dass mehrere Varianten gleichzeitig ausgeführt werden, gibt es in klassischen Algorithmen nicht.
Anforderung 3: Ausführbarkeit
Ausführbarkeit bedeutet, dass ein Prozessor jeden Einzelschritt des Algorithmus ausführen kann. Hier geht es also darum, was genau als «einzelner Schritt» gilt. Genau genommen hängt das natürlich vom Prozessor (oder vom Vorwissen des Lesers) ab. Bei der Formulierung von Algorithmen lässt man hier meist gesunden Menschenverstand walten: Jeder Schritt muss so klar und eindeutig formuliert sein, dass alle ihn gleich verstehen.
Anforderung 4: Endlichkeit
Endlichkeit bedeutet, dass der Algorithmus immer mit einer endlichen Anzahl Schritte zu einer Lösung kommt. Gerade mit Schleifen kann es schnell passieren, dass Algorithmen sehr viele Schritte haben. Eine unendliche Schleife darf jedoch unter keinen Umständen vorkommen, auch nicht für einen Sonderfall innerhalb der Problemklasse.
Anforderung 5: Korrektheit
Korrektheit bedeutet, dass der Algorithmus für alle möglichen Eingaben (bzw. für alle Probleme innerhalb der Problemklasse) in endlicher Zeit zu einer korrekten Lösung kommt. Die allgemeine Korrektheit eines Algorithmus zu verifizieren ist oft nicht einfach, vergleichbar mit Korrektheitsbeweisen in der Mathematik.
Algorithmen beschreiben
Natürliche Sprache: Ein sehr präzise formuliertes Rezept kann als Algorithmus gelten – aber es ist sehr schwer, sich mit normaler Sprache genau genug auszudrücken.
Programmiersprache: Ein Computerprogramm setzt immer einen Algorithmus um – verständlich ist das aber nur, wenn man die entsprechende Programmiersprache beherrscht und sich genau an deren Syntax hält.
Struktogramm: Als Kompromiss zwischen den beiden obigen Möglichkeiten formuliert man Algorithmen häufig in sogenannten «Struktogrammen».
Struktogramm
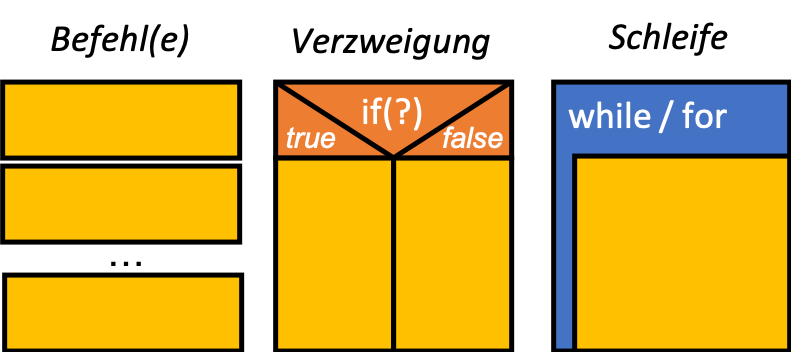
In einem Struktogramm formuliert man die einzelnen Anweisungen mit (möglichst präziser) natürlicher Sprache. Für die Darstellung der Reihenfolge der Anweisungen bedient man sich einiger grafischer Elemente, die sich an Ablaufstrukturen in Programmiersprachen anlehnen. Ein Struktogramm liegt also zwischen natürlicher Sprache und konkreter Programmiersprache; es muss nicht die genaue Syntax einer bestimmten Sprache berücksichtigen, ist aber recht einfach in eine beliebige Programmiersprache zu übersetzen – umgekehrt zwingt ein Struktogramm zum präzisen, schrittweisen Formulieren des Ablaufs und ist damit präziser und übersichtlicher als «normale» Sprache.
Als Alternative zu Struktogrammen kann man Algorithmen auch als Flow-Charts oder als Pseudocode formulieren. Aus Gründen der Einheitlichkeit und Kompaktheit halten wir uns in diesem Kurs an Struktogramme.
Struktogramme erstellt man meist als schnelle Skizzen mit Stift und Papier. Man kann aber auch ein Programm dafür benutzen, z.B. diesen Struktogrammeditor von Kevin Krummenauer.
Aufgabe
Im Aufgabenblatt KleineAlgorithmen.docx (pdf) geht es darum, einfache Algorithmen nachzuvollziehen oder selbst zu entwerfen – mithilfe von Struktogrammen.

 Algorithmen.pptx
Algorithmen.pptx