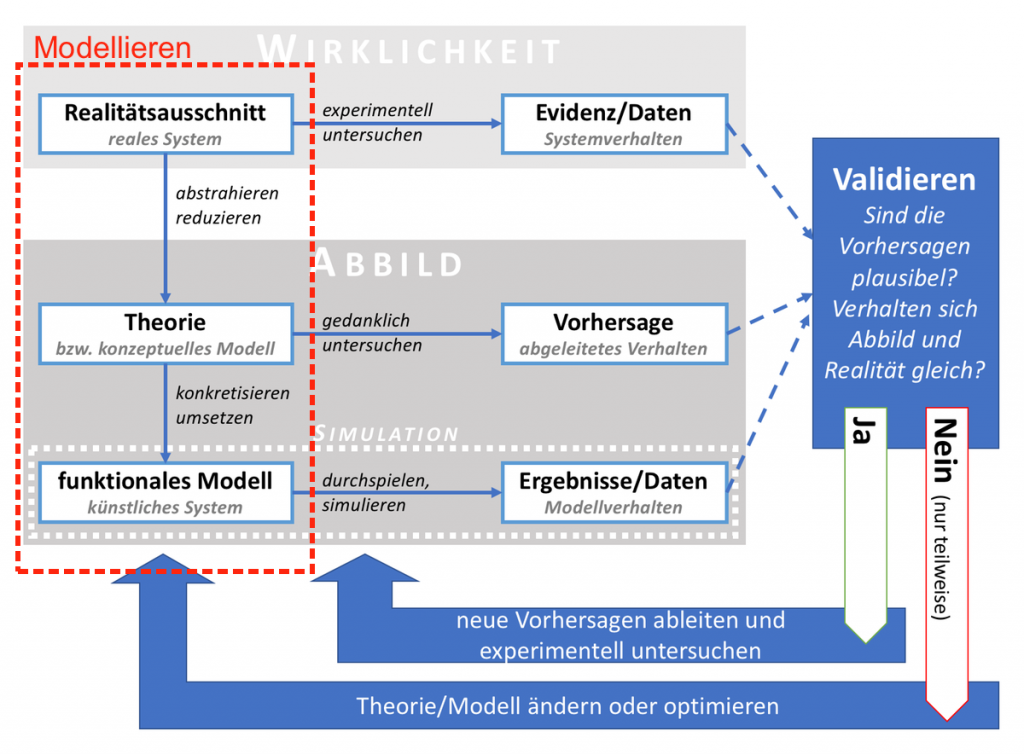
Modellieren
Modelle veranschaulichen Theorien, indem sie Teile der Realität imitieren. Zum Prozess der Modellierung gehört nicht nur das Imitieren, sondern vor allem auch die Festlegung des abgebildeten Realitätsausschnitts.
In vielerlei Hinsicht bedeutet Modell dasselbe wie Theorie – beide entwickeln ein Bild (eines Ausschnitts) der Realität, mit dem Zweck, diesen Wirklichkeitsausschnitt möglichst explizit zu beschreiben bzw. zu erklären. Ein Modell ist also eine Theorie in einer besonders anschaulichen Form.
Modell
Modell
Ein Modell ist ein abstraktes Abbild der Wirklichkeit, das wesentliche Aspekte enthält, jedoch aufgrund der Reduktion leichter zu untersuchen ist.
Quelle: Johannes Magenheim (2009), Informatik macchiato, S. 58
Eine solches Abbild (eines Ausschnitts) der Realität kann in verschiedenster Weise umgesetzt werden: als physische Nachbildung (z.B. ein Spielzeugauto), als schematische Zeichnung (z.B. Bohrsches Atommodell), als mathematische Formel (z.B. y = a*x + b als Modell einer Geraden) oder als Algorithmus (z.B. ein Neuronales Netz als Modell für menschliches Lernen).
In der Informatik wird eigentlich jeder Algorithmus, jedes Datenbankschema, jede Klasse als Modell bezeichnet, auch wenn in manchen Fällen nicht die Realität, sondern die virtuelle Welt eines Computerspiels damit abgebildet wird.
Viele Modelle sind hauptsächlich darauf ausgerichtet, das vorgeschlagene Abbild möglichst klar und unmissverständlich (also explizit) auszudrücken – z.B. als schematische Zeichnung, genormter Bauplan, mathematische Formel o.ä. Genau wie verbal formulierte Theorien müssen diese konzeptuellen Modelle vom Menschen interpretiert oder ausgerechnet werden, wenn man einen konkreten Zusammenhang zur Realität herstellen will – beispielsweise um abzuleiten, wie sich das Modell in einer ganz bestimmten Situation verhält.
Im Unterschied dazu gehen funktionale Modelle noch einen Schritt weiter: Die abgebildeten Eigenschaften, Funktionsweisen und Prozesse werden nicht nur genau beschrieben, sie werden in einem künstlichen System (z.B. einem Computerprogramm) umgesetzt. Dadurch kann man ein solches Modell mit konkreten Daten füttern und sein Verhalten in der dadurch spezifizierten Situation beobachten bzw. analysieren. Diesen Vorgang nennt man simulieren, er entspricht einem virtuellen Experiment.
Auch in einer weiteren wesentlichen Eigenschaft stimmen Theorie und Modell überein – es geht um die Einfachheit, also dass das Abbild weniger komplex ist als die Wirklichkeit. Der Erkenntnisgewinn steckt eben gerade in der Reduktion des Abbilds auf die wesentlichsten Einflussfaktoren und Zusammenhänge: Verhält sich das reduzierte Modell (fast) genauso wie die komplexe Realität, haben wir tatsächlich die wesentlichen Faktoren für eine einfache Erklärung identifiziert.
Nehmen wir beispielsweise an, wir wären in der Lage, ein vollständiges Abbild einer Maus zu konstruieren – bis hin zu jeder letzten Zelle, jeder chemischen Reaktion, jedem einzelnen Molekül und sogar Atom (zumindest letzteres ist übrigens nicht nur praktisch, sondern auch theoretisch unmöglich – das sagt zumindest die Heisenbergsche Unschärferelation, eine gut belegte Theorie aus der Teilchenphysik). In diesem Falle hätten wir eine künstliche Kopie der Maus erschaffen, die genauso komplex wäre, wie die reale Maus – der direkte Erkenntnisgewinn wäre gleich Null.
Allerdings kann u.U. auch ein komplexes Modell Erkenntnisse fördern. Das Kopieren der Maus hätte zwar unser Verständnis ihrer Funktionsweise oder Verhaltensmuster nicht erweitert, aber dafür lässt sich mit einer künstlichen Maus sehr viel besser experimentieren als mit einer echten (und viele Mäuseleben verschonen). Durch solch virtuelle Experimente am Modell lassen sich auf indirekte Weise doch Erkenntnisse gewinnen – und dieses Argument wird umso wichtiger, je aufwändiger oder unmöglicher Experimente am realen Untersuchungsgegenstand sind (z.B. Urknall).
Analogie
Ein Modell ist Abbild der Realität, versucht also zumindest in wesentlichen Aspekten wie die Realität zu sein – es ist also selbst eine Analogie der Realität. Eine Analogie dieser Analogie zu formulieren wäre vergleichbar damit, als Erklärung für ein Foto ein Foto von einem Foto zu machen, also wenig hilfreich – auch wenn das soeben geschehen ist.
Im Kontext dieses Kurses bzw. dem Thema Simulationen werden wir uns hauptsächlich mit funktionalen Computermodellen (engl. computational models) auseinandersetzen. Den Anspruch, explizit zu sein, erfüllen solche Modelle besonders gut, da sie letztendlich als Programmcode formuliert sein müssen. In der Folge werden zumeist solch algorithmisch umgesetzte, numerisch ausrechenbare, virtuelle Computermodelle gemeint sein, wenn von «Modell» die Rede ist.
Modellierung
Bevor man eine Simulation durchführen kann, muss man ein funktionales Computermodell entwickeln, also den relevanten Wirklichkeitsausschnitt modellieren. Das heisst, die Komplexität der Realität wird auf die wesentlichen Faktoren reduziert. Die Realität wird also nicht vollständig dargestellt. Diese Vollständigkeit ist aber gar nicht beabsichtigt, im Gegenteil: Es sollen lediglich die wesentlichen Einflussfaktoren identifiziert und dargestellt werden, die für den realen Prozess bedeutsam sind.
Der Prozess der Modellierung lässt sich grob in zwei Schritte unterteilen:
- Abstrahieren/Reduzieren: Der genaue Geltungsbereich bzw. Modellkontext muss definiert werden und die wesentlichen Einflussfaktoren bestimmt. Das Ziel ist ein möglichst einfaches Modell, das aber trotzdem die relevantesten Faktoren berücksichtigt.
- Konkretisieren/Umsetzen: Der Erklärungsansatz muss in ein funktionales Modell überführt werden, es gilt also, alle relevanten Eigenschaften und Funktionsweisen des reduzierten Abbilds als Programmcode – und damit maximal explizit – zu formulieren, genauer: als (auf verschiedene Klassen verteilte) Variablen und Methoden. Damit die Simulation bzw. das virtuelle Experiment dann konkret durchgespielt werden kann, müssen häufig auch relevante Aspekte der Umwelt bzw. des experimentellen Settings abgebildet, also modelliert werden.
Die wissenschaftliche Methode läuft auf eine kontinuierliche Weiterentwicklung von Theorien hinaus – das gilt natürlich auch für Modelle. Das Verhalten des Modells wird also mit dem Verhalten der Realität (=Evidenz) abgeglichen. In der Folge wird das Modell angepasst – also ein weiterer Durchlauf durch die obigen Modellierungsschritte vorgenommen – , so dass es im Laufe der Zeit zu einem immer besseren Abbild des relevanten Realitätsausschnitts wird und immer verlässlichere Vorhersagen über die Realität machen kann. Der Wert eines Modells beruht darauf, möglichst anschaulich und einfach zu sein – aus diesen Eigenschaften ergibt sich aber nur dann wissenschaftliche Erkenntnis, wenn aus dem Modell Aussagen über die abgebildete Realität abgeleitet werden können.

 SimulationenEinstieg.pptx
SimulationenEinstieg.pptx