Simulieren
Modelle in Bewegung versetzen und beobachten, was in welcher Situation passiert – das ist das Wesen der Simulation.
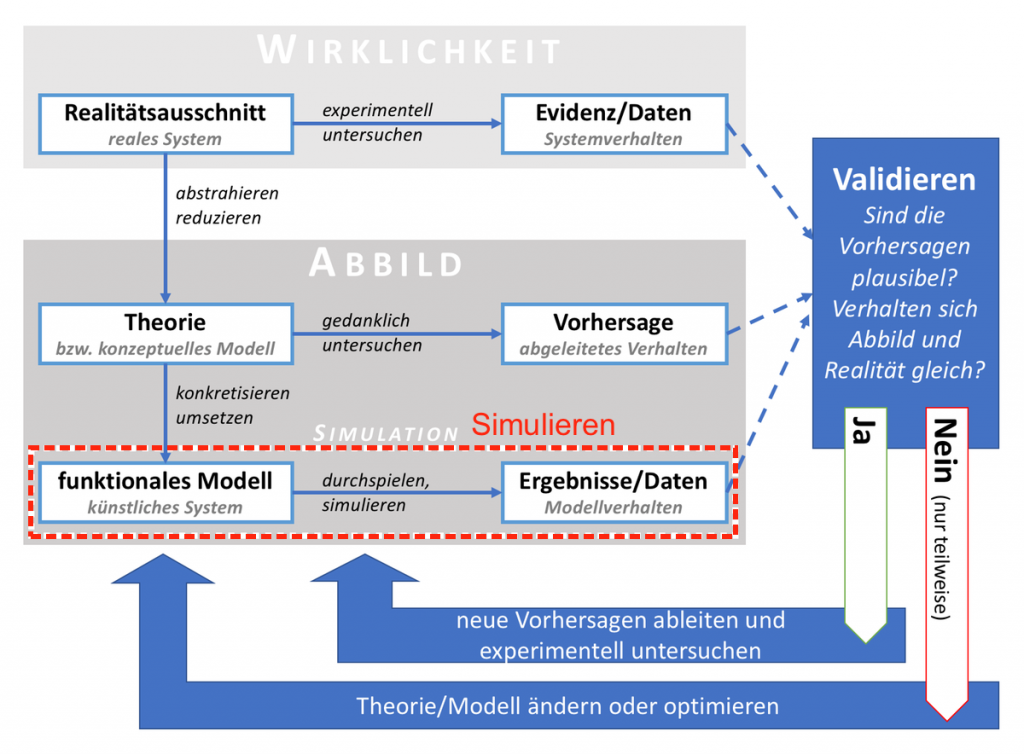
SimulationenEinstieg.pptxDie Simulation oder Simulierung ist eine Vorgehensweise zur Analyse von Abläufen in der Realität, die für die theoretische oder formelmässige Behandlung zu komplex sind, vor allem dann, wenn es sich um dynamisches Verhalten handelt. Konkret heisst das: Für die Simulation werden Experimente an einem Modell durchgeführt, um Erkenntnisse über die Realität zu gewinnen.
Durchgang
Im Zusammenhang mit Simulation spricht man von dem zu simulierenden System und von einem Simulator als Implementierung oder Realisierung eines Simulationsmodells. Letzteres stellt eine Abstraktion des zu simulierenden Systems dar (Struktur, Funktion, Verhalten). Der Ablauf des Simulators mit konkreten Werten (Parametrierung) wird als Simulationsexperiment bezeichnet. Dessen Ergebnisse können dann interpretiert und auf das zu simulierende System übertragen werden.
Simulieren bedeutet demnach, ein funktionales Modell in Bewegung zu versetzen und sein Verhalten in bestimmten Situationen zu beobachten. Je nach Komplexität des Modells kann dieser Vorgang langwierig und rechenintensiv sein – auch, weil ein einziger Durchgang selten genügt.
Parameter
Wie bei realen Experimenten versucht man in Simulationen meist, die Auswirkungen bestimmter Eigenschaften oder Rahmenbedingungen auf das Gesamtsystem zu untersuchen – dazu werden die Parameter in verschiedenen Durchläufen variiert.
Parameter
Parameter – (deutsch) auch Übergabewert genannt – sind in der Informatik Variablen, durch die ein Computerprogramm (oft ein Unterprogramm) auf die Verarbeitung bestimmter Werte «eingestellt» werden kann. Parameter sind also programmextern gesetzte Einflussfaktoren; sie werden insbesondere beim Aufruf von Unterprogrammen verwendet, um diesen ‚mitzuteilen‘, welche Daten/Werte sie verarbeiten sollen und ggf. wie.
Durch Parametrisierung können Programme in ihrer Anwendung flexibilisiert werden, ohne dass das Programm dazu neu erstellt werden muss. Welche Werte eingestellt werden können, muss bei der Erstellung von Programmen festgelegt werden. Parameter können z. B. bestimmte Grenzwerte/Auswahlbedingungen (für Beträge, ein Datum oder ähnliches) oder zu verwendende Texte sein oder auch das «Was» und das «Wie» der Verarbeitung steuern (z. B. Prüfung X vornehmen – ja/nein).
Quelle: Wikipedia, Parameter (Informatik)
Auch der Begriff «Parameter» wird nicht in allen Fach- oder Anwendungsgebieten gleich verstanden – die obige Definition bezieht sich auf die allgemeine Verwendung des Begriffs in der Informatik (z.B. in Bezug auf Übergabewerte einer Methode). Im Kontext von Simulationen bezeichnen Parameter diejenigen Aspekte eines Modells, die bewusst flexibel angelegt wurden. Indem das Modell mit konkreten Werten für diese Parameter gefüttert wir, versetzt man es in eine bestimmte Situation oder einen bestimmten Zustand und simuliert dann das Verhalten.
Analogie
Ein Plattenspieler ist eine ziemlich komplizierte Maschine, deren Verhalten (= abgespielte Töne) in der Hauptsache von zwei variablen Faktoren (=Parametern) abhängt: Der aufgelegten Schallplatte und der eingestellten Rotationsgeschwindigkeit des Plattentellers.
Ein Durchgang der Simulation erfordert die Festlegung konkreter Werte für alle Parameter. In einem typischen virtuellen Experiment wird in mehreren Durchgängen der Wert für einen der Parameter variiert, so dass sich die ggf. unterschiedlichen Ergebnisse auf den Einfluss genau dieses Parameters zurückführen lassen. Komplizierter wird es, wenn mehrere Parameter systematisch variiert werden müssen – insbesondere wenn es darum geht, Interaktionen zwischen den Parametern zu verstehen.
Zufallswerte
Neben der gezielten Variation von Parametern gibt es noch einen weiteren Grund dafür, dass in Simulationen oft sehr viele Durchgänge nötig sind: stochastische Parameter. Häufig ist es sinnvoll, bestimmte Eigenschaften des Anfangszustands einer Simulation zufällig festzulegen – oder ein Modell befolgt in jeder Runde mit einer bestimmten Wahrscheinlichkeit die eine oder andere Regel. Enthält eine Simulation solche Zufallselemente (stochastischen Parameter), ist ein einzelner Durchgang nur bedingt aussagekräftig, da das Ergebnis ja zumindest zu einem gewissen Grad durch Zufall zustande kam. Es braucht also mehrere Wiederholungen, um das «typische» Verhalten des Modells in dieser Situation (mit ansonsten unveränderten Parametern) abzuschätzen. Und auch die Zufallselemente können an (Meta-)Parameter gekoppelt sein – z.B. könnte es Sinn machen, die Wahrscheinlichkeit für die Befolgung einer bestimmten Regel systematisch zu variieren.
Beim Simulieren versetzt man das funktionale Modell in Bewegung, indem man es mit konkreten Werten füttert. Die systematische Variation von Parametern der Simulation ist der Kern dieser Phase.