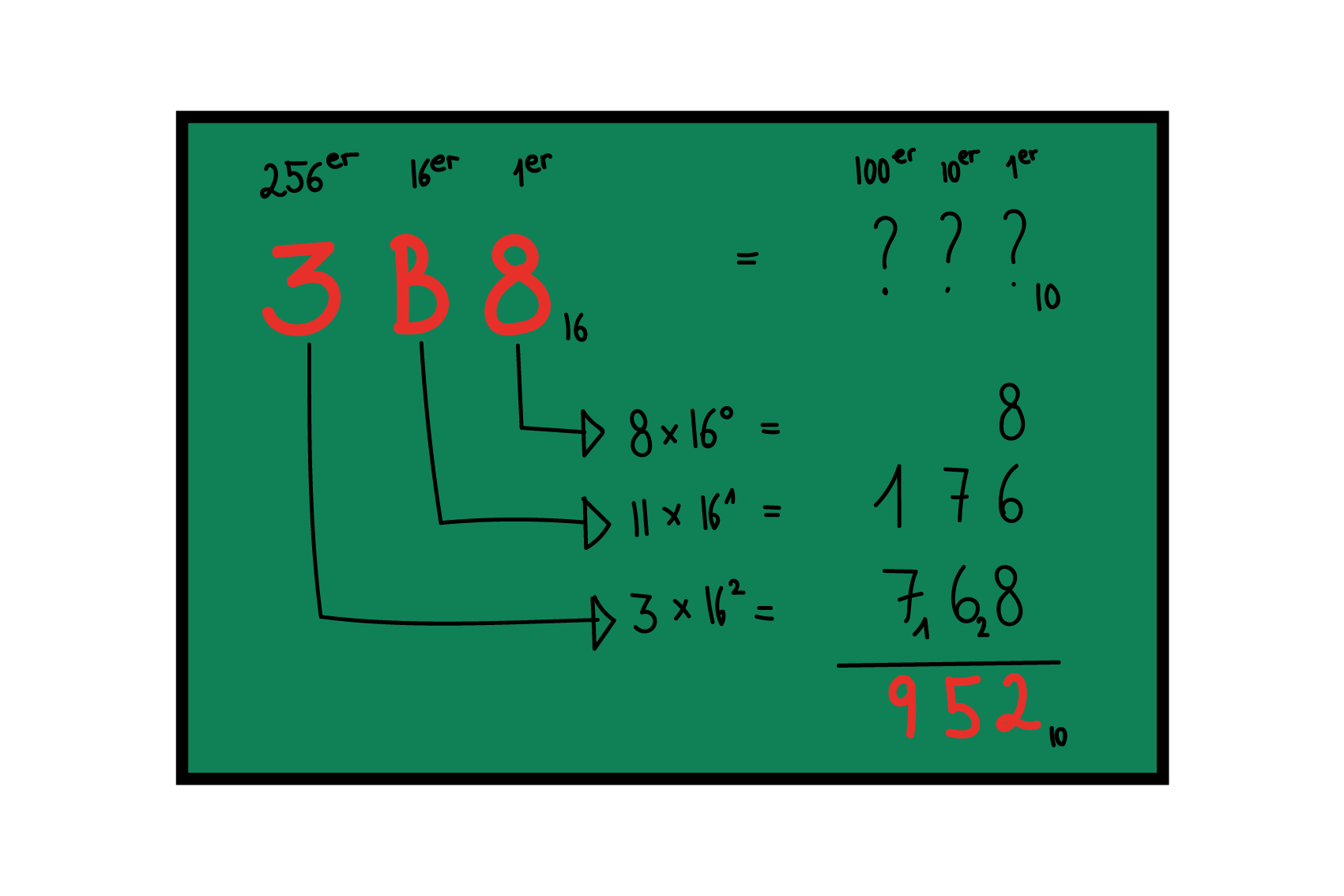Binärsystem
(Oder wie Computer die Welt sehen)
MATERIALIEN
Um Informationen festhalten zu können, braucht es einen Code. Wörter zum Beispiel oder Zahlen. Der Computer arbeitet mit einem binären Code.
Fangfrage: Wie weit können Sie mit zehn Fingern zählen?
Antwort: Schlau gemacht bis 1023 (210-1).
Die Fangfrage verdeutlicht, dass beim Zählen zwei Aspekte zusammenspielen: Eine Anzahl unterschiedlicher Ziffern und eine Anzahl Stellen, die mit diesen Ziffern belegt werden können. Nur durch die Kombination dieser zwei Aspekte kann man beliebig weit zählen und – in der Folge – mit beliebig grossen Zahlen geschickt rechnen.
Noch bevor der erste Computer tatsächlich gebaut wurde, hat Alan Turing bewiesen, dass eine solche universelle Rechenmaschine tatsächlich alles berechnen kann (d.h. alles, was berechenbar ist, wenn jemand den richtigen Algorithmus programmiert hat und wenn genügend Zeit zur Verfügung steht). Aus eher praktischen Gründen ist die Grundlage dieser universellen Rechenfähigkeit von Computern das Binärsystem.
Binärsystem
Wie der Name schon andeutet, unterscheidet sich das Binärsystem vom in der Mathematik gebräuchlicheren Dezimalsystem nur dadurch, dass es zwei statt zehn Ziffern verwendet – die Systematik ist genau gleich.
Binärsystem
Als Binärsystem bezeichnet man das Zahlensystem, das mit Basis 2, also mit nur zwei Ziffern arbeitet. Diese Ziffern werden meist als 0 und 1 repräsentiert, aber eigentlich geht es nur darum, dass ein Bit zwei verschiedene Zustände haben kann.
Eine Stelle im Binärsystem nennt man ein Bit, als Konvention hat es sich eingebürgert, 8 Bit als ein Byte zu bezeichnen.
Analogie
Mit einer Hand kann man bis fünf zählen, wenn man jeden Finger als eine Ziffer interpretiert. Sieht man aber jeden Finger als eine Stelle mit zwei Zuständen (Finger ist ausgestreckt oder nicht), dann arbeitet man im Binärsystem und kann bis 25-1, also bis 31 zählen.
Zahlensysteme
Das uns allen bekannte Dezimalsystem ist eine grossartige Erfindung, auf deren Basis sich nicht nur die moderne Mathematik entwickelt hat, sondern auch die meisten Wissenschaften und Technologien. Das Entscheidende am Dezimalsystem ist allerdings die Systematik der Stellenwerte. Dass Zahlen üblicherweise aus zehn unterschiedlichen Ziffern (=dezimal) aufgebaut werden, ist reine Konvention. Wahrscheinlichster Grund: Wir haben zehn Finger.
Als System funktioniert ein solches Stellenwertsystem immer gleich – sowohl fürs Zählen als auch fürs Rechnen –, auch wenn es auf 16 (hexadezimal), acht (oktal) oder nur zwei (binär) Ziffern basiert.
Letzteres war für die Entwicklung einer universellen Rechenmaschine (Computer) entscheidend, weil sich zwei Ziffern (= 1 Bit) viel einfacher physisch umsetzen lassen als beispielsweise zehn.
Analogie
Wäre Herr Al-Chwarizmis (ein arabischer Gelehrter, auf den die Einführung des modernen Dezimalsystems oft zurückgeführt wird) ein Alien mit nur zwei Fingern gewesen, dann würden heute wohl alle Menschen (nicht nur die Computer) im Binärsystem rechnen.
Dass Computer mit Bits arbeiten ist praktisch, weil sich ein Bit durch verschiedenste physische Zustände umsetzen lässt – z.B.:
- Strom / kein Strom (Arbeitsspeicher);
- positive / negative Polung (Festplatte);
- Licht an / aus (Glasfaserkabel);
- Laser reflektiert / reflektiert nicht (CD oder DVD);
- Murmel / keine Murmel (Murmelrechner Video & Interactive), u.ä.
Zählen oder rechnen lässt sich im Binärsystem genau gleich wie in jedem anderen Zahlensystem.
Allerdings muss am Computer immer schon im Vorhinein festgelegt sein, wie viele Stellen eine Zahl (oder sonstige Information) beanspruchen darf, und deswegen braucht es oftmals die Überlegung, wie grosse Zahlen (bzw. wie viele unterschiedliche Möglichkeiten) sich mit einer bestimmten Anzahl Bits darstellen lassen.
Kombinationen
Nicht nur am Computer ergibt sich immer wieder die Frage, wie viele verschiedene Kombinationsmöglichkeiten von Zeichen oder Ziffern sich für eine bestimmte Anzahl Stellen ergeben. Die Antwort ist immer dieselbe:
Möglichkeiten pro Stelle hoch Anzahl Stellen
Beispiele:
- Wenn ein Passwort aus 4 Kleinbuchstaben besteht, dann gibt es insgesamt 264 = 456976 verschiedene Passwörter (ein Hacker könnte diese Kombinationen mithilfe einer brute-force Attacke sehr schnell alle durchprobieren)
- Wenn die Farbe eines Pixels mit 3 Byte, also 24 Bit codiert ist, dann kann dieses Pixel 224 = ca. 16.7 Mio unterschiedliche Farben haben
- Wenn eine Dezimalzahl 3 Stellen lang ist, dann gibt es 103 = 1000 verschiedene Möglichkeiten. Weil die Null auch eine dieser Möglichkeiten ist, können wir mit drei Stellen von 0 bis 999 zählen
Achtung! Die Frage nach der höchsten Zahl, die in eine bestimmte Anzahl Stellen passt, ist nur fast dasselbe wie die Frage nach der Anzahl der Kombinationen. Wie in Beispiel 3 ersichtlich wird, muss man für die höchste Zahl noch 1 abziehen – weil man ja bei Null angefangen hat. Geht es beispielsweise um die höchste Dezimalzahl, die sich mit einem Byte speichern lässt, dann ist die Antwort: 28-1 = 255.
Analogie
Die DNA einer einzelnen menschlichen Zelle enthält etwa 3.27 Milliarden Basenpaare. Für jedes Basenpaar gibt es 4 Möglichkeiten (A/T/G/C).
Insgesamt gibt es also ca. 43270000000 = 26540000000 Zustände, welche ein solcher DNA-Strang annehmen könnte.
Dieser Speicher entspricht somit rund 6.54 Milliarden Bit, also 817.5 Millionen Byte oder 817.5 Megabyte resp. ca. 779 MiB.
Wieviel fasst Ihre Festplatte zuhause?
Aufgaben zu Zahlensystemen
Aufgabe
Im Interactive Basis 10 zu 2 üben Sie das Umrechnen einer Dezimalzahl in eine Binärzahl – optional kann man versuchen, das besonders schnell zu schaffen.
Aufgabe
Im Aufgabenblatt BinäreDaten.docx (pdf) üben Sie den Umgang mit verschiedenen Codierungen (im ersten Teil geht es um Zahlen).
Aufgabe
Interaktives Umrechnen zu Dezimalzahlen üben Sie mit den Interactives Basis 2 zu 10 (Binär-), Basis 3 zu 10 (Tertiär-) oder Basis 16 zu 10 (Hexadezimalzahlen).
Versuchen Sie bspw., eine Dezimale 13 zu erzielen, oder 27, 84, 342, …
Aufgabe
Für Profis: Umrechnen üben zwischen dem Zehner- und einem (fast) beliebigen anderen System im Interactive Basis N zu M.

 BitsBytes.pptx
BitsBytes.pptx