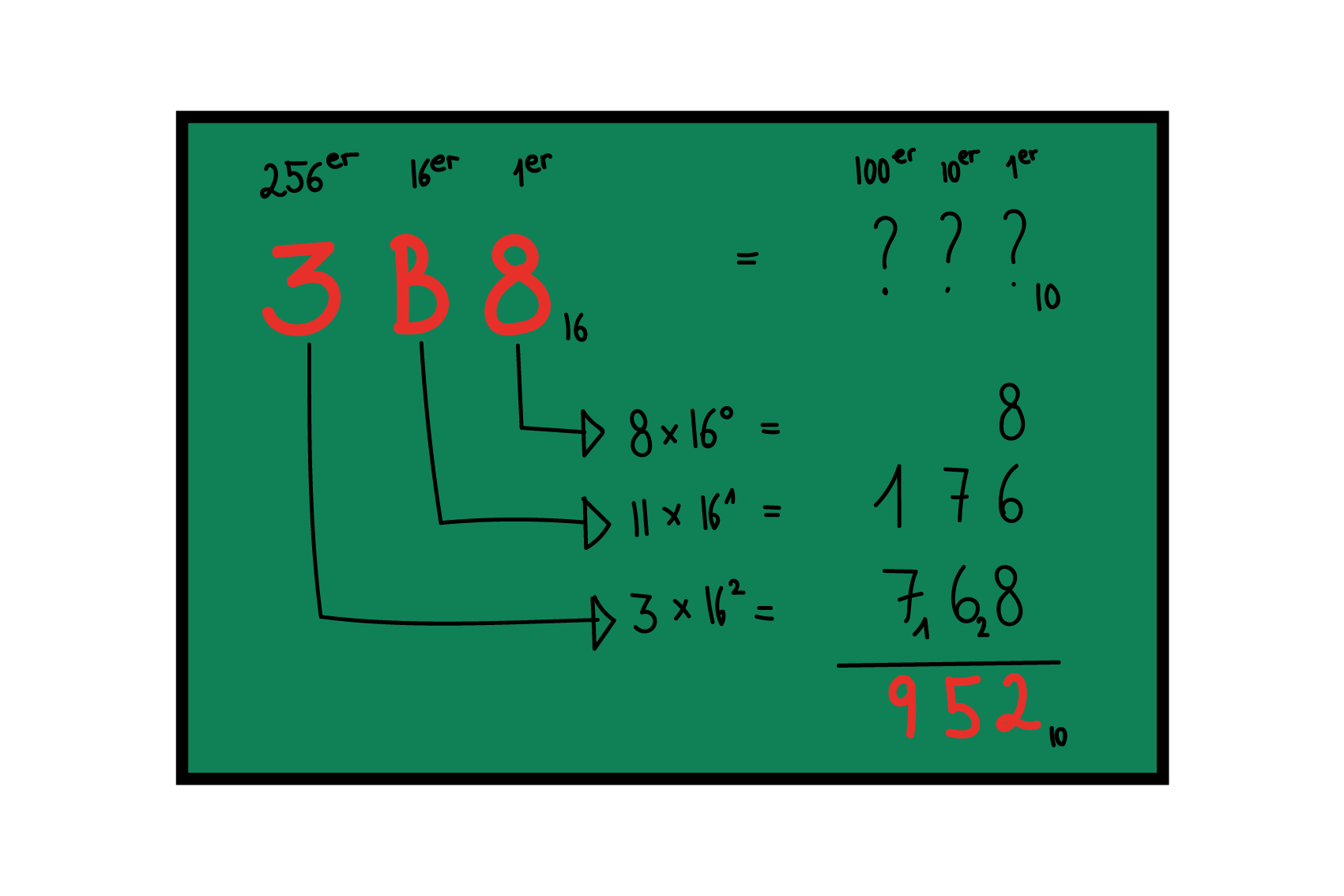Im Schweizer Bundesgesetz über den Datenschutz (DSG) ist festgelegt, dass die rechtmässige Bearbeitung von Personendaten Daten prinzipiell erlaubt ist, solange folgende Grundsätze eingehalten werden:
Konzepte
Beispielkonzept
Ein Konzept beschreibt eine fundamentale Idee des Fachgebiets, also ein allgemeines Denk-, Handlungs-, Beschreibungs-, oder Erklärungsschema, das in verschiedenen Bereichen oder Anwendungen des Fachgebiets zugrundeliegt und längerfristige Gültigkeit hat. Im Einzelnen sollte ein Konzept folgende Anforderungen erfüllen:
- Horizontalkriterium: Das Konzept sollte in verschiedenen Bereichen vielfältig anwendbar oder erkennbar sein
- Vertikalkriterium: Das Konzept sollte auf verschiedenen intellektuellen Niveaus oder Abstraktionsgraden aufgezeigt und vermittelt werden können
- Zeitkriterium: Das Konzept sollte in der historischen Entwicklung deutlich wahrnehmbar sein und auch in Zukunft längerfristig relevant bleiben
- Sinnkriterium: Das Konzept sollte einen Bezug zu Sprache und Denken des Alltags aufweisen, bzw. Entsprechungen in der realen Welt haben
vgl. Andreas Schwills Definition unter www.informatikdidaktik.de/Forschung/Schriften/ZDM.pdf
Fachgebiet Informatik
Der Begriff «Informatik» bezeichnet ein Fachgebiet (Schulfach, Studienrichtung, Berufszweig), das sich mit den Grundlagen der automatischen Informationsverarbeitung beschäftigt.
Fachgebiet: Es geht um eine wissenschaftliche Herangehensweise, beweisbare Fakten und grundlegende, übertragbare Konzepte.
Automatische Verarbeitung: Eine Lösungsvorschrift (=Algorithmus) wird von einer programmierbaren Maschine (Computer) umgesetzt.
Information: Informationen werden digitalisiert (als digitale Daten repräsentiert) und in dieser Form gespeichert, kopiert, versendet, dargestellt, verrechnet oder allgemein gesagt: verarbeitet.
Klasse vs. Instanz
Beim objektorientierten Programmieren wird der zu einer Software gehörende Code auf verschiedene Module, sogenannte «Klassen» verteilt. Üblicherweise entspricht eine Klasse einer Datei, die den entsprechenden Programmiercode enthält.
Binärsystem
Als Binärsystem bezeichnet man das Zahlensystem, das mit Basis 2, also mit nur zwei Ziffern arbeitet. Diese Ziffern werden meist als 0 und 1 repräsentiert, aber eigentlich geht es nur darum, dass ein Bit zwei verschiedene Zustände haben kann.
Zahlensysteme
Das uns allen bekannte Dezimalsystem ist eine grossartige Erfindung, auf deren Basis sich nicht nur die moderne Mathematik entwickelt hat, sondern auch die meisten Wissenschaften und Technologien. Das Entscheidende am Dezimalsystem ist allerdings die Systematik der Stellenwerte. Dass Zahlen üblicherweise aus zehn unterschiedlichen Ziffern (=dezimal) aufgebaut werden, ist reine Konvention. Wahrscheinlichster Grund: Wir haben zehn Finger.
Als System funktioniert ein solches Stellenwertsystem immer gleich – sowohl fürs Zählen als auch fürs Rechnen –, auch wenn es auf 16 (hexadezimal), acht (oktal) oder nur zwei (binär) Ziffern basiert.
Dateiformat
Ein Dateiformat definiert die Syntax (Aufbau) und die Semantik (Inhalt) von Daten innerhalb einer Datei. Es stellt damit eine bidirektionale Abbildung von Information auf einen eindimensionalen binären Speicher dar.
Quelle: https://de.wikipedia.org/wiki/Dateiformat
Ein Dateiformat kann also als Sammlung von Regeln für die Reihenfolge und die Codierung(en) von Daten verstanden werden.
Diese Regeln braucht man in zwei Richtungen:
- Wenn man Informationen in einer Datei ablegen will (=Codierung).
- Wenn man Daten in Form einer Datei bekommt und diese als Information interpretieren will (=Decodieren).
Damit das funktionieren kann,
- müssen diese Definitionen (Regeln) für ein Dateiformat bekannt sein (zumindest den Programmierern);
- muss für jede Datei klar sein, welcher Regelsatz (Dateityp) verwendet wird (diese Informationen kann meist der Dateiendung und/oder dem Header entnommen werden).
Algorithmus
Ein Algorithmus ist eine eindeutige Handlungsanweisung für die Lösung von Problemen. Algorithmen bestehen aus endlich vielen, wohldefinierten Einzelschritten. Sie können in menschlicher Sprache formuliert oder aber zur Ausführung in ein Computerprogramm implementiert werden. Für die Problemlösung wird eine bestimmte Eingabe Schritt für Schritt in eine bestimmte Ausgabe überführt.
Codierung
Um sehr einfache Informationen zu codieren (z.B. den Wahrheitsgehalt einer logischen Aussage) braucht es ggf. nur ein Bit. Für komplexere Informationen (z.B. die genaue Angabe einer Farbe) werden mehrere Bit kombiniert. Mehrere Bit bzw. eine Bit-Sequenz repräsentieren also einen Sachverhalt (einen Zustand, eine Information) mithilfe eines zugrundeliegenden Systems – der Codierung. Um von den Daten auf die repräsentierten Informationen schliessen zu können, muss man die Art der Codierung kennen.
Struktogramm
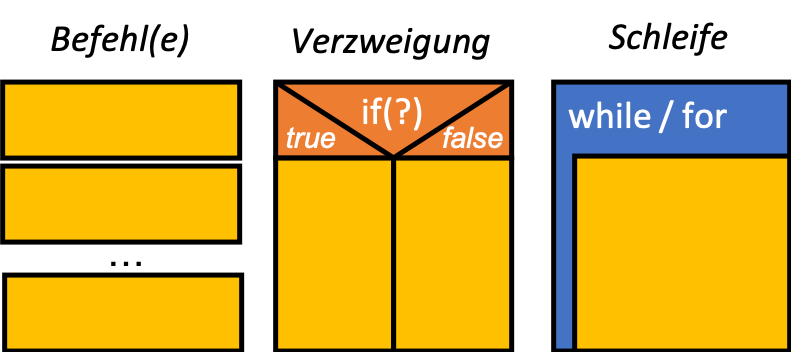
In einem Struktogramm formuliert man die einzelnen Anweisungen mit (möglichst präziser) natürlicher Sprache. Für die Darstellung der Reihenfolge der Anweisungen bedient man sich einiger grafischer Elemente, die sich an Ablaufstrukturen in Programmiersprachen anlehnen. Ein Struktogramm liegt also zwischen natürlicher Sprache und konkreter Programmiersprache; es muss nicht die genaue Syntax einer bestimmten Sprache berücksichtigen, ist aber recht einfach in eine beliebige Programmiersprache zu übersetzen – umgekehrt zwingt ein Struktogramm zum präzisen, schrittweisen Formulieren des Ablaufs und ist damit präziser und übersichtlicher als «normale» Sprache.
Computational Thinking
Computational Thinking (auf Deutsch etwa «Informatisches Denken») beschreibt ein sehr allgemeines Set von Denkfiguren (= Arten des Denkens), die bei der Problemlösung zum Einsatz kommen. Computational Thinking bezieht sich nicht notwendigerweise auf Algorithmen und auch nicht nur auf die Informatik. Vielmehr sollen die beschriebenen Denkweisen als Hilfestellung zur strukturierten Lösung aller möglichen Arten von Problemen dienen.
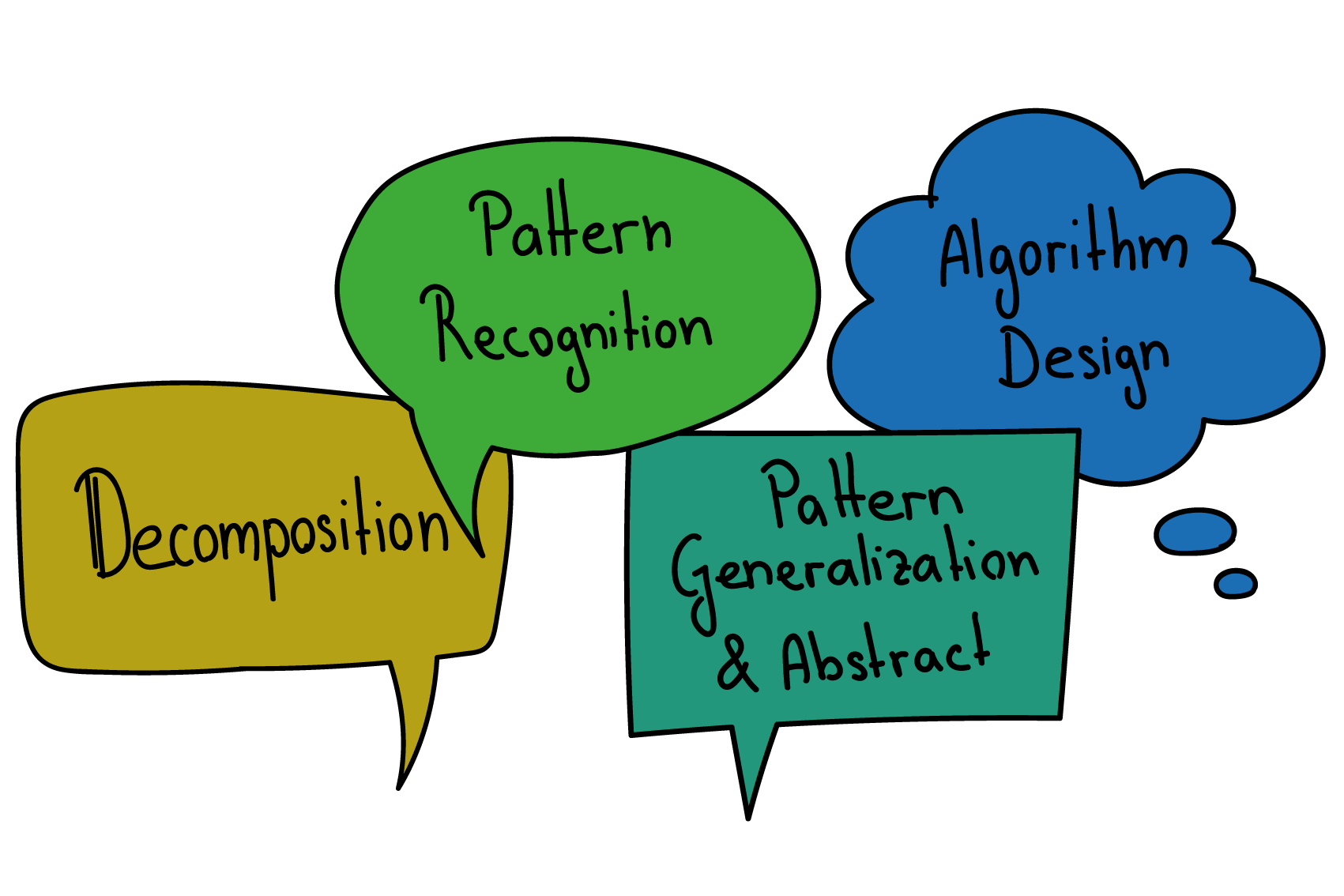
Die wichtigsten Denkfiguren des Computational Thinking sind:
- Decomposition: Ein grosses Problem wird in mehrere kleine zerlegt. Diese kleineren Teilprobleme sind einfacher zu handhaben bzw. zu bedenken, oft kann man sie einzeln nacheinander lösen. Dazu gehört ebenfalls die Strategie, zunächst eine einfachere Version des Problems zu lösen und den initialen Lösungsansatz dann auf immer allgemeinere Formen des Problems zu erweitern.
- Pattern Recognition: Wiederkehrende Muster und ähnliche Teilprobleme, also gleichartige Strukturen werden identifiziert. So kann man sich bei der Lösungsfindung auf wenige Aspekte konzentrieren und durch die wiederholte Anwendung derselben Lösungsschritte auch umfangreiche Aufgaben meistern.
- Abstraction: Das Problem wird aus einem gewissen Abstand betrachtet und über Details hinweggeschaut. Dieser Schritt ist beispielsweise nötig, um das Problem in seiner einfachst möglichen Form zu formulieren, in der nur noch die wirklich relevanten Informationen berücksichtigt werden.
Natürlich hilft die abstraktere Sichtweise auch bei Decomposition und Pattern Recognition, denn oftmals zeigt sich, dass zu Beginn verschieden erscheinende (Teil-)Probleme sich auf einen gemeinsamen Kern zurückführen lassen und mit derselben (wiederholten) Strategie zu lösen sind.
Bei komplexen Problemen ist es oft nötig, kontinuierlich mit verschiedenen Ebenen der Abstraktion umzugehen, beispielsweise wenn man eigentlich gerade eine Lösung für ein Teilproblem sucht, dabei aber den Zusammenhang mit dem Gesamtproblem auf der einen und der technischen Umsetzung auf der anderen Seite nicht ganz ausser Acht lassen darf. - Algorithm Design: Die Lösung oder den Lösungsansatz wird in klar formulierte, einzelne Schritte aufgeteilt und eine Reihenfolge für diese Schritte festgelegt. Dazu gehört ebenfalls, dass man die Rahmenbedingungen für einen Algorithmus immer wieder überprüft (z.B. ob die Schritte eindeutig formuliert sind, ob der gefundene Lösungsansatz immer korrekte Ergebnisse liefert oder ob alle Varianten des Problems berücksichtigt sind).
Monte Carlo Methode
Die Monte Carlo Methode bezeichnet eine Vorgehensweise zur (beliebig genauen) Annäherung an die Lösung schwieriger Probleme, bei der man sich den Zufall zunutze macht. Im Kern geht es darum, „Experimente“ mit zufälligen Eingabewerten zu machen und aus den Ergebnissen die „wahre“ Antwort abzuleiten. Die Antwort wird mit zunehmender Anzahl der Experimente bzw. Testfällen immer genauer und verlässlicher (Gesetz der Grossen Zahlen). Die Monte Carlo Methode ist am nützlichsten für Probleme, bei denen eine analytische Lösung nur schwer oder gar nicht möglich ist.
Laufzeitkomplexität
Unter der Zeitkomplexität eines Problems versteht man die Anzahl der Rechenschritte, die ein Algorithmus zur Lösung dieses Problems benötigt, in Abhängigkeit von der Länge der Eingabe (bzw. der Grösse des Problems). Man spricht hier auch von der asymptotischen Laufzeit und meint damit – in Anlehnung an eine Asymptote – das Zeitverhalten des Algorithmus für eine potenziell unendlich grosse Eingabemenge. Es interessiert also nicht der Zeitaufwand eines konkreten Programms auf einem bestimmten Computer für ein bestimmtes Problem, sondern vielmehr, wie der Zeitbedarf wächst, wenn mehr Daten zu verarbeiten sind. Die Frage ist also z.B., ob sich der Aufwand für die doppelte Datenmenge verdoppelt oder quadriert (Skalierbarkeit). Weniger wichtige Faktoren (z.B. Konstanten) spielen dabei keine Rolle und werden üblicherweise ignoriert.
Bei der Abschätzung der Zeitkomplexität geht man üblicherweise vom „worst case“ aus, man berücksichtigt also die Anzahl Rechenschritte, die benötigt werden, wenn das spezielle Problem innerhalb der Problemklasse maximal ungünstig gewählt ist.
Datenstruktur
Eine Datenstruktur fasst mehrere Werte unter einem Namen zusammen und ermöglicht so, dass Computerprogramme flexibel und effizient auch mit grösseren Datenmengen umgehen können. Die üblichsten Datenstrukturen kann man sich vorstellen wie eine Liste (bzw. eine Tabelle) – dabei werden die einzelnen Werte durch einen Index adressiert (ähnlich wie in Excel).
Modularisierung
Unter Modularisierung versteht man das Aufteilen eines komplexen Systems (oder Aufgabe, Organisation, Ablauf, usw.) in kleinere, in sich abgeschlossene Bestandteile – sogenannte “Module”. Module sollten voneinander möglichst unabhängig sein, abgesehen vom Austausch der absolut notwendigen Informationen über wohldefinierte Schnittstellen. Auf diese Weise können die einzelnen Module innerhalb des Gesamtsystems flexibel miteinander kombiniert werden und gemeinsam komplizierte Aufgaben lösen – und gleichzeitig spielt es für das Gesamtsystem eigentlich keine Rolle, wie genau das Modul selbst arbeitet.
Schichtenmodell
Bei einem Schichtenmodell sind mehrere Module (s. Modularisierung) hierarchisch verknüpft. Jede «Schicht» kann also nur mit der jeweils über oder unter ihr liegenden Schicht kommunizieren – wieder über eine wohldefinierte Schnittstelle.
Durch diesen Aufbau ergeben sich unterschiedliche (Abstraktions-)Ebenen, und jede Schicht muss sich nur um ihre eigene Ebene kümmern.
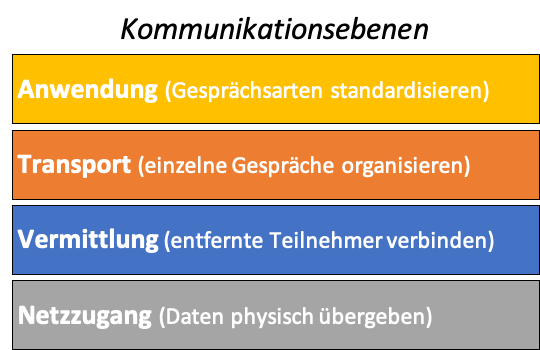
Kommunikationsebenen
Eine Kommunikation zwischen zwei Digitalgeräten besteht eigentlich aus mehreren ineinander verschachtelten Gesprächen. Das Internet konnte seine explosionsartige Entwicklung nur deshalb so verhältnismässig reibungslos überstehen, weil die verschiedenen «Gespräche» schon früh mithilfe eines sauberen Schichtenmodells auf verschiedene Kommunikationsebenen aufgeteilt wurden.
(Das theoretische Schichtenmodell der digitalen Kommunikation heisst OSI, im Internet wird zumeist die etwas vereinfachte TCP/IP-Protokollfamilie benutzt.)
Datenpakete
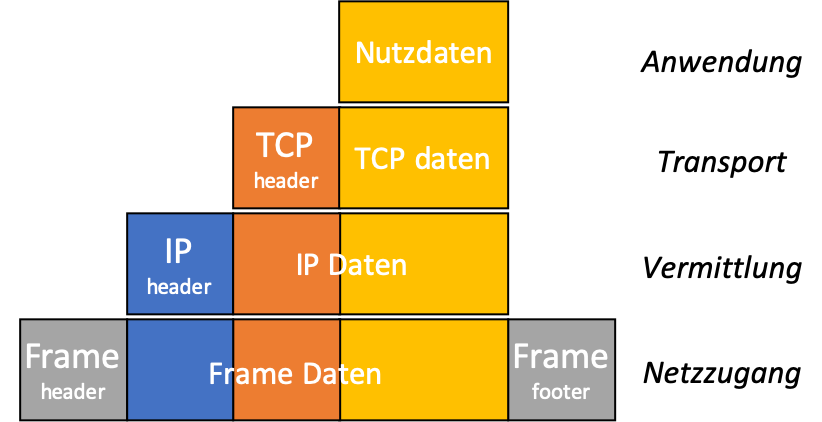
Datenpakete bestehen aus zwei Bestandteilen:
- Die Daten, die eigentlich transportiert werden sollen, nennt man «payload». Pro Paket können nicht sehr viele Daten transportiert werden, üblicherweise gilt ein Maximum von 1500 Byte (=1,5 KB) pro Paket – die meisten Dateien müssen also aufgeteilt und in vielen einzelnen Paketen durch das Internet geschickt werden. Je nachdem, worum es bei der Kommunikation geht, kann es sich bei der payload beispielsweise um den HTML-Code einer Webseite handeln, oder um einen Teil einer JPG-Datei, oder um ein paar Millisekunden eines gestreamten YouTube-Clips.
- Damit die Pakete ihren Weg durch das Netz finden, braucht es noch weitere Informationen, sogenannte Metadaten. Die Metadaten von Netzwerkpaketen enthalten Informationen wie beispielsweise die Quell- und die Ziel-IP, oder eine Sequenznummer, die angibt, dass dieses Paket das fünfte von insgesamt 17 ist, die zu einer bestimmten Nachricht gehören.
Diese Informationen sind natürlich standardisiert (wie Formate), die zugehörigen Bits werden zumeist vor der payload eingefügt (header) – bei manchen Protokollen kommen auch noch einige Bit ans Ende, deshalb spricht man allgemeiner von einem frame.
Protokoll
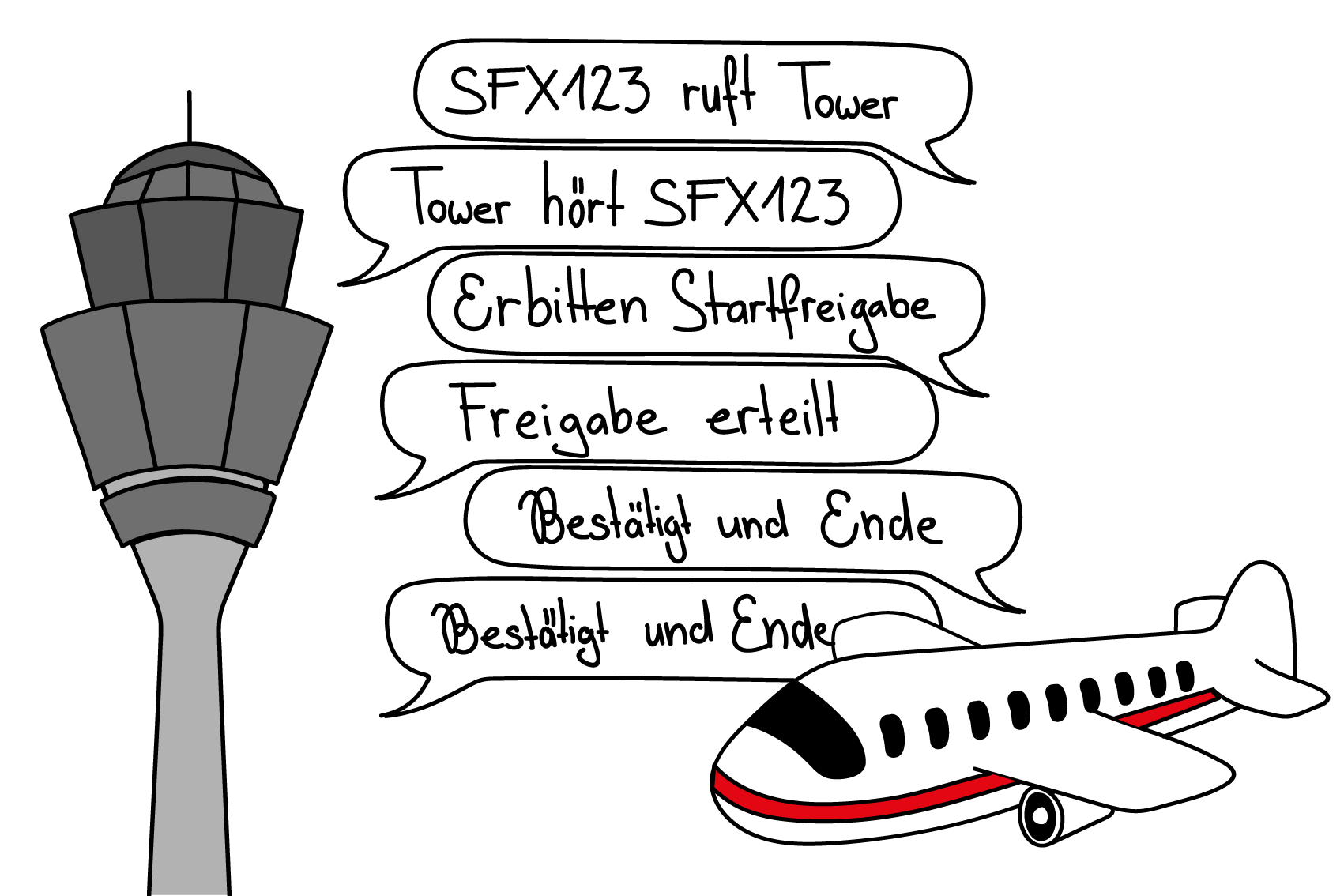
Die Kommunikation zwischen Computern folgt immer standardisierten Vorgehensweisen, geregelt durch Protokolle für jede Kommunikationseben. Ein Protokoll regelt bzw. definiert
- den zeitlichen Ablauf der Kommunikation und
- das Format der einzelnen Nachricht(en), bestehend aus Metadaten (im header) und der eigentlichen Nachricht (= payload).
Nur wenn sich alle Beteiligten an die Protokolle halten, können die übertragenen Bit richtig interpretiert werden.
Für die Kommunikation im Internet definiert die TCP/IP-Protokollfamilie die für die jeweilige Kommunikationsebene einsetzbaren Protokolle, die sich jeweils um die auf dieser Ebene relevante Adressierung kümmern:
Application/Anwendung (Client ⟺ Server)
Standardisierte Gespräche zwischen Programmen ermöglichen
Transport (Port ⟺ Port)
Datenpakete verwalten (Bestätigung, Reihenfolge, Zuordnung zu Gesprächen, …)
Internet/Vermittlung (IP ⟺ IP)
Transport von Datenpaketen zwischen Client und Server – über Subnetze hinweg
Data Link/Netzzugang (MAC ⟺ MAC)
Übergabe der Daten von einer Netzwerkkarte zu nächsten (z.B. per Kabel, WiFi, Satellit, ...)
Subnetz
Mehrere Geräte befinden sich dann in einem gemeinsamen Subnetz, wenn
- eine physikalische Verbindung zwischen ihnen besteht (z.B. Kabel, WiFi, usw.) und
- ihre IPs mithilfe einer entsprechenden Netzmaske als zur selben Gruppe gehörend definiert wurden.
Alle an einem Subnetz beteiligten Geräte können direkt Nachrichten austauschen, nur wenn die Nachricht in ein anderes Subnetz gelangen soll, braucht es dafür einen Router (der Mitglied in mehreren Subnetzen ist). Subnetze bilden die logische Struktur des Internets (= Netz der Netze), sie ermöglichen die flexible, weltweite Kommunikation zwischen Digitalgeräten (s. Routing).
Physikalische Adresse
Die physikalische Adresse, auch Hardware-Adresse eines Computers – genauer gesagt: seiner Netzwerkkarte – nennt man MAC-Adresse (das hat nichts mit Apple zu tun, sondern steht für media access control). Sie besteht aus 48 Bit, die man üblicherweise als Hexadezimalzahl mit 6×2 Stellen angibt, bspw: 48-2C-6A-1E-59-3D. Jede MAC-Adresse muss weltweit eindeutig sein, sie wird schon bei der Herstellung der Netzwerkkarte fix eingebaut.
MAC-Adressen sind essentiell für die digitale Kommunikation, weil Datenpakete ausschliesslich von einer Netzwerkkarte an eine andere weitergegeben werden können, also von einer MAC an eine andere.
Logische Adresse
Im Gegensatz zur physikalischen Adresse ist die logische Adresse – die IP – eines Geräts einstellbar – das ermöglicht beispielsweise die flexible Gruppierung (s. Netzmaske) oder den reibungslosen Austausch eines defekten Geräts (MAC ändert sich, IP nicht). Trotzdem muss die IP (zumindest innerhalb eines Intranets) eindeutig sein, weil andernfalls nicht klar ist, an wen eine Nachricht gehen soll.
Eine IPv4 besteht aus vier Byte, in der üblichen dezimalen Darstellung sieht das dann bspw. so aus:
IPv4: 192.168.0.17 (jeder Block kann Werte zwischen 0 und 255 haben).
DNS
Das Domain Name System (DNS) ist dafür zuständig, die in einer URL gebräuchlichen Domains in IPs zu übersetzen – das erfordert eine separate DNS-Anfrage an den DNS-Server, der in den Systemeinstellungen eingetragen ist. Falls dieser die Domain nicht auflösen kann, fragt er einen übergeordneten DNS-Server, bis spätestens der für die Top Level Domain (z.B. xyz.ch) zuständige DNS-Server die gesuchte IP bereitstellt.
URL
Der Inhalt des WWW (world wide web) entspricht einem riesigen Haufen von Dokumenten (Webseiten, etc.), die über das Internet abgerufen werden können. Eine URL (uniform resource locator) dient dazu, die Adresse für eines dieser Dokumente eindeutig anzugeben.
Genau genommen ist die URL ein Pfad, der sich aus drei Teilen zusammensetzt:
- Das Protokoll (der Anwendungsschicht), hier steht meist http oder https (=verschlüsselt)
- Die Domain, also die logische Adresse des Servers (übersetzbar in und auch ersetzbar duch eine IP)
- Alles nach der TDL ist ein lokaler Pfad auf dem Server, genau wie auf der eigenen Festplatte
Client - Server
Umgangssprachlich nennt man oft den Computer des Benutzers den Client, und den Computer, auf dem die abgerufene Webseite gespeichert ist, den Server. Genaugenommen bezieht sich die Bezeichnung «Client» aber immer auf ein Programm, das eine Information anfragt, und «Server» auf ein Programm, das die Anfrage beantwortet. So gibt es beispielsweise während des Aufrufs einer Webseite vielfältige Client-Server-Beziehungen:
- Der Browser erfragt Webseite (per URL), das Betriebssystem holt die Seite aus dem Internet.
- Das Betriebssystem erfragt die zur URL gehörende IP, der DNS-Server beantwortet diese Anfrage.
- Das Betriebssystem erfragt die zu einer IP gehörende MAC (per ARP), das für die IP zuständige Gerät im Subnetz antwortet mit seiner MAC.
Routing
Die Grundidee der (flexiblen) digitalen Vernetzung besteht darin, dass manche Computer – sogenannte Router – Mitglied in mehr als nur einem Netzwerk sind – in jedem mit einer eigenen Netzwerkkarte (und MAC). Router haben dadurch die Möglichkeit, Datenpakete in einem Netzwerk zu empfangen und sie in ein anderes Netzwerk weiterzuleiten. So kann ein Datenpaket von einem (Sub-)Netz ins nächste weitergereicht werden und auf diese Weise in wenigen Millisekunden von einem Ende der Welt zum anderen gelangen. Das geht so schnell, weil im sogenannten «backbone» des Internets einige vielbeschäftigte Router in weltumspannenden (Sub-)Netzen zusammengeschlossen sind, so dass ein Paket beispielweise in einem einzigen Schritt vom DE-CIX in Frankfurt durch ein Glasfaserkabel am Grund des Ozeans an den NYIIX in New York gelangen kann. So kann ein Datenpaket über eine Handvoll von Zwischenstationen («Hops») zu jedem anderen mit dem Internet verbundenen Computer geleitet werden.
Router arbeiten mit sogenannten Routingtabellen, in denen Regeln festgehalten sind, die festlegen, in welches (Sub-)Netz ein Paket mit einer bestimmten logischen Adresse (IP) weitergegeben wird – die eigentliche Weitergabe erfolgt dann aber über die physikalische Adresse (MAC).
ARP
Datenpakete können immer nur von einer MAC an die nächste weitergegeben werden. Oft kennt man aber nur die logische Adresse des nächsten Empfängers. In diesem Fall kommt das ARP (adress resolution protocol) zum Einsatz: Per broadcast-MAC werden alle Mitglieder des Subnetzes gefragt, wer denn für die gesuchte IP zuständig sei, und nur das betreffende Gerät antwortet mit seiner MAC.
Netzmaske
Mithilfe der Netzmaske kann man verschiedene IPs flexibel zu Gruppen zusammenfassen. Das Prinzip ist simpel: Die Netzmaske gibt an, wie viele Stellen (von links gezählt) übereinstimmen müssen, damit zwei IPs zum selben Subnetz gehören. Beispielsweise besagt die Netzmaske 255.255.255.0, dass die IPs in den ersten drei Bytes übereinstimmen müssen – das letzte Byte (also 256 Werte) kann dann benutzt werden, um die zu diesem Subnetz gehörenden IPs zu unterscheiden.
Datenbanksystem
Ein Datenbanksystem (DBS) ist eine Zusammenfassung von strukturierten Daten (Datenbank, DB), die von einer speziellen Software (Data Base Management System, DBMS) verwaltet und über eine definierte Schnittstelle vielen Nutzern oder Anwendungen gleichzeitig und kontrolliert zur Verfügung gestellt werden.
Hardware
Unter Hardware versteht man die elektronisch oder mechanisch arbeitenden Komponenten eines Computersystems. Dazu gehört beispielsweise die CPU, in der die eigentlichen Berechnungen stattfinden, verschiedene Arten von Speichern (Register, Caches, RAM, Festplatte), aber auch alle Arten von digitalen Geräten, die man an den Computer anschliessen kann (sogenannte Peripheriegeräte, z.B. Tastatur, Maus, Bildschirm, Drucker, usw.)
Software
Der Begriff Software entstand ursprünglich in Abgrenzung zum Begriff Hardware und bezieht sich daher auf alle nicht-physischen Bestandteile eines Computers. Im allgemeinen Sprachgebrauch hat sich inzwischen eingebürgert, Software als Sammelbegriff für alle von einem Computer ausführbaren Programme (inklusive zugehöriger Daten, wie z.B. Icons oder Schriften) zu benutzen. Zur Software zählen neben den Anwendungsprogrammen, die man auf einem Computer installieren kann, auch jene Programme, die zum Betriebssystem gehören und die moderne Computer überhaupt erst so flexibel nutzbar machen.
Betriebssystem
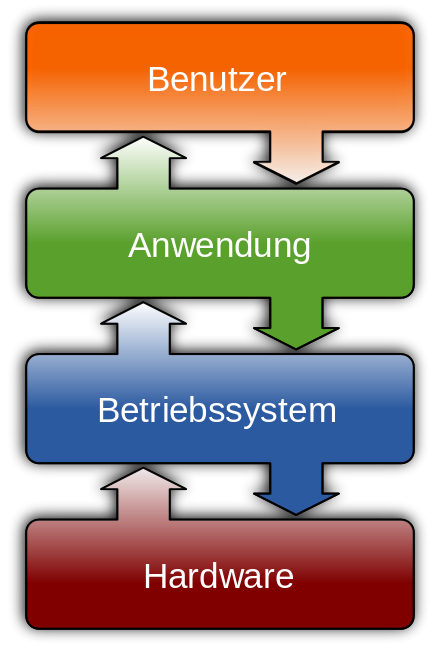
Das Betriebssystem (z.B. Windows , MacOS oder eine der vielen Linux-Varianten) ist selbst eine Software – man kann es auf eine DVD brennen oder aus dem Internet herunterladen und auf verschiedenen Computern installieren – aber es hat sehr spezielle Aufgaben: in der Hauptsache ist das Betriebssystem dafür zuständig, dass andere Programme die Hardware des Computers komfortabel benutzen können.
Der Aufbau der meisten Computersysteme entspricht demnach einem Schichtenmodell, s. nebenstehende Abbildung.
Computerarchitektur
Auch heute noch richtet sich der Aufbau fast aller gängigen Computer nach einem 1945 erstmals vorgestellten Referenzmodell, der nach ihrem Erfinder benannten «Von Neumann-Architektur». Diese Architektur beschreibt die Verbindung (über einen BUS) eines Prozessors (CPU) und seiner drei integralen Bestandteile (Steuerwerk/CU, Rechenwerk/ALU, und Speicherwerk/Memory Unit) mit einem Arbeitsspeicher (RAM), in dem – und das ist die Besonderheit – sowohl die auszuführenden Befehle als auch die zu verarbeitenden Werte (in binärer Form) gespeichert sind. Weil die Befehle auch nur Daten sind, können beide in einem Programm (in Maschinensprache) flexibel kombiniert werden und somit auf ein und derselben Hardware die verschiedensten Algorithmen umsetzen.
Malware
Der Begriff «Malware» setzt sich aus dem lateinischen Wort für «schlecht» und dem Begriff «software» zusammen und kann ins Deutsche am besten mit «Schadprogramm» oder «Schadsoftware» übersetzt werden.
Malware kann als Oberbegriff für jegliche Software verstanden werden, die entwickelt wurde, um – meist vom Nutzer unbemerkt – unerwünschte bzw. schädliche Funktionen auf dessen Rechner auszuführen.
Obwohl Schadsoftware schon zu Beginn des Computerzeitalters von Bedeutung war, führt die größere Verbreitung und Bedeutung der sogenannten neuen Medien und deren vermehrt sorgloserer Umgang zu einem vergrößerten Bedrohungspotential. Die möglichen Schäden sind vielseitig und reichen von Angriffen auf die Privatsphäre über üble Scherze, Betrug und Erpressung, bis hin zur Zerstörung wichtiger PC-Bauteile. Die meisten Schadprogramme verstecken sich jedoch auf dem infizierten Computer, um unbemerkt längerfristige Ziele verfolgen zu können. Die Bandbreite reicht vom sich aggressiv verbreitenden «Computerwurm» über neugierige «Spyware» bis hin zu «Trojanern», deren Zweck eine Fernsteuerung des Zielrechners ist.
Symmetrische Verschlüsselung
Unter dem Begriff Symmetrische Verschlüsselung fasst man alle Kryptosysteme zusammen, bei welchen zur Ver- und Entschlüsselung derselbe Schlüssel verwendet wird.
Der Sender verschlüsselt also die Nachricht mit dem gemeinsamen Schlüssel. Der Geheimtext wird anschliessend übermittelt und der Empfänger dekodiert diesen mit demselben Schlüssel. Das bedeutet auch, dass dieser Schlüssel ebenfalls übermittelt, aber unbedingt geheim bleiben muss. Darin liegt auch ein Hauptproblem: Sender und Empfänger müssen sich auf einen gemeinsamen Schlüssel einigen, ohne dass ein Dritter auf den Schlüssel zugreifen kann.
Häufigkeitsanalyse
Die Häufigkeitsanalyse ist eine der Methoden, die statistische Eigenschaften von verschlüsselten Texten ausnutzen, um Rückschlüsse auf die unverschlüsselte Nachricht zu ziehen.
In jeder Sprache kommen die einzelnen Buchstaben in einem ausreichend langen Text in einer für die Sprache charakteristischen Häufigkeit vor. Im Deutschen ist der am häufigsten vorkommende Buchstabe das E (etwa 17%), gefolgt von N (ca. 10%), I und R (je ca. 8%). Ersetzt man also in einer verschlüsselten Nachricht das am häufigsten vorkommende Zeichen mit E, und die nächsthäufigsten mit N, I und R, dann hat man gute Chance, schon ca. die Hälfte des Textes übersetzt zu haben.
Asymmetrische Verschlüsselung
Bei einer Asymmetrischen Verschlüsselung gibt es zwei verschiedene, aber zusammengehörige Schlüssel:
- Der public key kann nur für die Verschlüsselung verwendet werden, deswegen muss er auch nicht geheim sein
- Der private key wird für die Entschlüsselung verwendet, er bleibt geheim, muss aber nie an den Kommunikationspartner geschickt werden
Grob gesagt geht der Ablauf so: Wer verschlüsselte Nachrichten empfangen will, rechnet sich ein Schlüsselpaar aus – einen öffentlichen (Public Key) und einen privaten (Privat Key). Den Public Key kann er nun an einem öffentlich zugänglichen Ort (z.B. Server) hinterlegen oder auf Anfrage herausgeben. Der Sender benutzt diesen Public Key, um mithilfe einer einfachen Rechnung eine Bitsequenz (=Klartext) in eine verschlüsselte Sequenz zu übersetzen – dann kann er diese Geheimnachricht an den Empfänger schicken. Zum Entschlüsseln muss jetzt die einfache Rechnung von oben rückgängig gemacht werden – das geht aber nur mit Kenntnis des zugehörigen Privat Key. Diesen kennt natürlich der Urheber des Schlüsselpaars, sonst aber niemand, denn der Privat Key musste ja nie an irgendwen übermittelt werden.
Einwegfunktion
Unter einer Einwegfunktion versteht man in der Informatik eine mathematische Funktion, die ressourcensparend zu berechnen, aber sehr schwer umzukehren ist.
Das «sehr schwer» im obigen Satz bedeutet genau dasselbe wie in der folgenden Aussage: «Ein gutes Passwort ist nicht unmöglich zu erraten, aber sehr schwer.» Das Problem besteht in beiden Fällen nicht darin, dass der Lösungsweg (=Algorithmus) unbekannt ist, sondern darin, dass das Finden/Berechnen der Lösung schlicht zu lange braucht. Wie lange genau, hängt von der Rechengeschwindigkeit ab – das ist aber wenig relevant, weil weder Millionen noch Milliarden von Jahren als angemessene Zeit für das Erraten eines Passworts oder für das Knacken einer Verschlüsselung gelten können.
Digitale Zertifikate
Ein digitales Zertifikat dient dazu, die Authentizität eines öffentlichen Schlüssels und seinen zulässigen Anwendungs- und Geltungsbereich zu bestätigen. Das digitale Zertifikat ist selbst durch eine digitale Signatur geschützt, deren Echtheit mit dem öffentlichen Schlüssel des Ausstellers des Zertifikates geprüft werden kann. Um die Authentizität des Ausstellerschlüssels zu prüfen, wird wiederum ein digitales Zertifikat benötigt. Auf diese Weise lässt sich eine Kette von digitalen Zertifikaten aufbauen, die jeweils die Authentizität des öffentlichen Schlüssels bestätigen, mit dem das vorhergehende Zertifikat geprüft werden kann. Eine solche Kette von Zertifikaten wird Validierungspfad oder Zertifizierungspfad genannt. Das letzte Element (das Root-Zertifikat) gehört zu einer Zertifizierungsstelle und kann nicht weiter überprüft werden, die Zertifizierungsstelle ist also die Wurzel der Vertrauenskette.
Zertifikate sind im Wesentlichen digitale Beglaubigungen. Somit stellt das Vertrauen zwischen dem Prüfer und dem Aussteller eines Zertifikates sowie die Art und Weise, wie dieses Vertrauen zustande kommt, die wesentliche Basis für die Verwendung digitaler Zertifikate dar. Umgekehrt lassen sich solche Vertrauensmodelle in der Regel erst durch Zertifikate technisch umsetzen. Das gesamte System hinter der Validierung von Zertifikaten nennt man public-key-infrastructure.
Privatsphäre
Privatsphäre bezeichnet den nichtöffentlichen Bereich, in dem ein Mensch unbehelligt von äußeren Einflüssen sein Recht auf freie Entfaltung der Persönlichkeit wahrnimmt. Das Recht auf Privatsphäre gilt als Menschenrecht und ist in allen modernen Demokratien verankert. Dieses Recht kann aufgrund des öffentlichen Interesses an einer Person oder zu Zwecken der Strafverfolgung eingeschränkt werden.
Quelle: Wikipedia
Allgemeine Erklärung der Menschenrechte
Art. 12: «Niemand darf willkürlichen Eingriffen in sein Privatleben, seine Familie, sein Heim oder seinen Briefwechsel noch Angriffen auf seine Ehre und seinen Beruf ausgesetzt werden. Jeder Mensch hat Anspruch auf rechtlichen Schutz gegen derartige Eingriffe oder Anschläge.»
Phishing
Beim Phishing geht es um eine sehr menschliche Art von Sicherheitsproblem: Wenn jemand an meine Login-Daten kommt, dann kann er meine digitale Identität übernehmen und in den entsprechenden Anwendungen all das tun, was eigentlich nur ich können sollte. Mögliche Folgen reichen von verärgerten Freunden (z.B. weil Sie auf Sozialen Netzwerken in meinem Namen beleidigt werden) über Verletzungen der Privatsphäre (z.B. weil ein Fremder jetzt Zugang zu meinen persönlichen Daten, zu peinlichen Bilder, zu intimen Geheimnissen hat) bis hin zu finanziellen Verlusten (z.B. weil jemand Zugriff auf meine Kreditkartendetails oder mein Online-Banking hat). Die gravierendsten Folgen ergeben sich meist, wenn die findigen Phisher über die kompromittierte Identität Zugang erhalten zu Firmennetzwerken, internen Datenbeständen, Staatsgeheimnissen, o.ä.
Metadaten
Als Metadaten bzw. Metainformationen werden strukturierte Daten bezeichnet, die Informationen über andere Informationsressourcen enthalten. Metadaten beschreiben also die eigentlichen Daten auf eine Art und Weise. Metainformationen werden erforderlich, wenn es größere Datenmengen zu verwalten gibt. Ein ausgesprochenes Merkmal von Metadaten ist daher oft, dass sie maschinell lesbar und auswertbar sind.
Quelle: Andreas Pfund, Metadaten
Filterblase
Die Filterblase (englisch filter bubble) oder Informationsblase ist ein Begriff, der vom Internetaktivisten Eli Pariser in seinem gleichnamigen Buch von 2011 verwendet wird. Laut Pariser entstehe die Filterblase, weil Webseiten versuchen, algorithmisch vorauszusagen, welche Informationen der Benutzer auffinden möchte – dies basierend auf den verfügbaren Informationen über den Benutzer (beispielsweise Standort des Benutzers, Suchhistorie und Klickverhalten). Daraus resultiere eine Isolation gegenüber Informationen, die nicht dem Standpunkt des Benutzers entsprechen.
Quelle: Wikipedia, Filterblase
Big Data
Der aus dem englischen Sprachraum stammende Begriff Big Data (von englisch big ‚groß’ und data ‚Daten’) bezeichnet Datenmengen, welche beispielsweise zu groß, zu komplex, zu schnelllebig oder zu schwach strukturiert sind, um sie mit manuellen und herkömmlichen Methoden der Datenverarbeitung auszuwerten. Im deutschsprachigen Raum ist der traditionellere Begriff Massendaten gebräuchlich.
«Big Data» wird häufig als Sammelbegriff für digitale Technologien verwendet, die in technischer Hinsicht für eine neue Ära digitaler Kommunikation und Verarbeitung und in sozialer Hinsicht für einen gesellschaftlichen Umbruch verantwortlich gemacht werden.
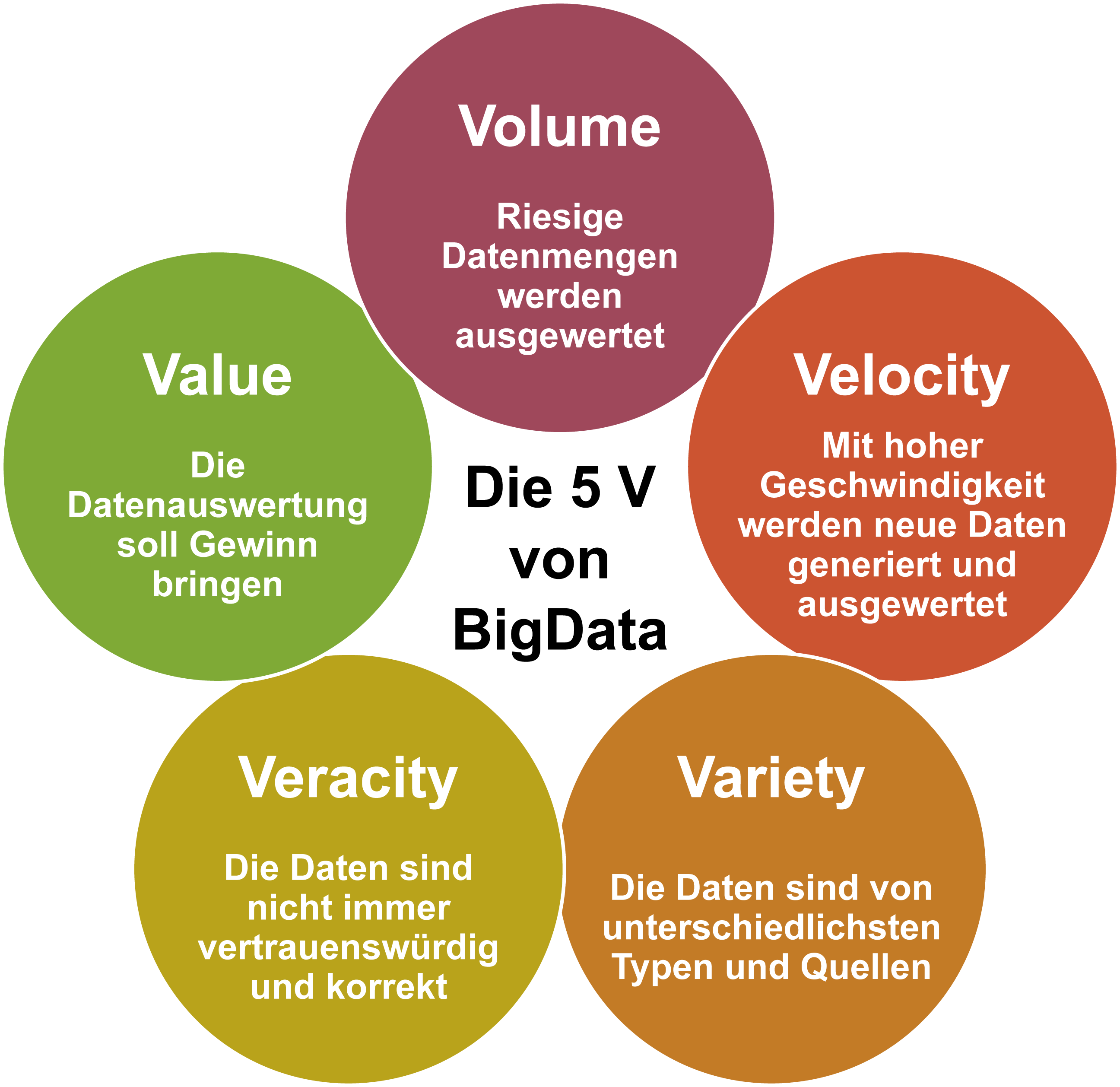
In der Definition von Big Data bezieht sich das «Big» auf die drei Dimensionen volume (Umfang, Datenvolumen), velocity (Geschwindigkeit, mit der die Datenmengen generiert und transferiert werden) sowie variety (Bandbreite der Datentypen und -quellen). Erweitert wird diese Definition um die zwei V value und validity, welche für einen unternehmerischen Mehrwert und die Sicherstellung der Datenqualität stehen.
Quelle: Wikipedia, Big Data (16.06.2019)
Maschinelles Lernen
Maschinelles Lernen ist ein Oberbegriff für die «künstliche» Generierung von Wissen aus Erfahrung: Ein künstliches System lernt aus Beispielen und kann diese nach Beendigung der Lernphase verallgemeinern. Das heißt, es werden nicht einfach die Beispiele auswendig gelernt, sondern es «erkennt» Muster und Gesetzmäßigkeiten in den Lerndaten. So kann das System auch unbekannte Daten beurteilen (Lerntransfer).
Quelle: Wikipedia, Maschinelles Lernen
Theorie
In der Wissenschaft bezeichnet Theorie ein System wissenschaftlich begründeter Aussagen, das dazu dient, Ausschnitte der Realität und die zugrundeliegenden Gesetzmäßigkeiten zu erklären und Prognosen über die Zukunft zu erstellen. Im Allgemeinen entwirft eine Theorie ein Bild (Modell) der Realität. In der Regel bezieht sie sich dabei auf einen spezifischen Ausschnitt der Realität. Eine Theorie enthält in der Regel beschreibende (deskriptive) und erklärende (kausale) Aussagen über diesen Teil der Realität. Auf dieser Grundlage werden Vorhersagen getroffen.
Quelle: Wikipedia, Theorie
Salopper formuliert: Eine Theorie ist eine begründete (aber nicht bewiesene!) Erklärung für reale Phänomene oder Prozesse. Um wissenschaftlichen Ansprüchen zu genügen, muss eine Theorie zudem einige Minimalanforderungen erfüllen:
- Eine wissenschaftliche Theorie muss explizit sein, d.h. es muss Einigkeit darüber bestehen, was genau die vorgeschlagene Erklärung ist.
- Eine wissenschaftliche Theorie muss widerspruchsfrei sein, d.h. die Erklärungen und Zusammenhänge müssen in sich konsistent sein.
- Eine wissenschaftliche Theorie muss überprüfbar sein, d.h. sie muss sich anhand von Evidenz be- insbesondere aber auch widerlegen lassen.
Evidenz
In der Wissenschaftstheorie bezeichnet der Begriff «Evidenz» zumeist diejenigen empirischen Befunde, die Theorien bestätigen oder aufgrund derer Bestätigungsversuche scheitern.
Quelle: Wikipedia, Evidenz
Simulation
Menschen haben schon im Altertum begonnen, Naturphänomene mit allgemeingültigen Regeln zu beschreiben (Theorie). Mit der Zeit führten genauere Beobachtungen und gezielte Experimente zu Verbesserungen der Theorie und zu entsprechenden Berechnungsformeln. Für praktische Anwendungen waren diese Formeln allerdings oft zu komplex, sodass Näherungslösungen genügen mussten und manche Berechnungen gar nicht möglich waren. Erst seit der Verfügbarkeit von Rechenautomaten (also nach dem Zweiten Weltkrieg) konnten anspruchsvolle reale Sachverhalte genügend genau durch rein virtuelle, numerische Modelle repräsentiert werden (Simulation). Virtuelle Modelle sind insbesondere dort wichtig, wo materielle Experimente extrem teuer oder gar nicht möglich sind.
Virtuelle Modelle und Simulationen bilden heute neben Theorie und Experiment das dritte Standbein der wissenschaftlichen Erkenntnis in allen naturwissenschaftlichen und technischen Disziplinen sowie bereits auch in manchen Bereichen der Wirtschafts- und Sozialwissenschaften.
Quelle: Jürg Kohlas, Jürg Schmid, Carl August Zehnder (2013)
Bei einer Simulation wird die Theorie in ein numerisches Modell überführt, es wird also mithilfe von Algorithmen genau spezifiziert, wie welche Daten verarbeitet werden sollen. Auch die zu verarbeitenden Informationen – oft Referenzdaten genannt – müssen genau festgelegt werden, üblicherweise indem aus realen Experimenten oder Messungen gewonnene Evidenz digital angenähert oder sogar direkt eingespeist wird. Auf diese Weise überführt man die beiden wesentlichen Aspekte der wissenschaftlichen Methodik in ein virtuelles System und kann so die Interaktion aller Komponenten aktiv ausprobieren – eben simulieren.
Modell
Ein Modell ist ein abstraktes Abbild der Wirklichkeit, das wesentliche Aspekte enthält, jedoch aufgrund der Reduktion leichter zu untersuchen ist.
Quelle: Johannes Magenheim (2009), Informatik macchiato, S. 58
Eine solches Abbild (eines Ausschnitts) der Realität kann in verschiedenster Weise umgesetzt werden: als physische Nachbildung (z.B. ein Spielzeugauto), als schematische Zeichnung (z.B. Bohrsches Atommodell), als mathematische Formel (z.B. y = a*x + b als Modell einer Geraden) oder als Algorithmus (z.B. ein Neuronales Netz als Modell für menschliches Lernen).
Parameter
Parameter – (deutsch) auch Übergabewert genannt – sind in der Informatik Variablen, durch die ein Computerprogramm (oft ein Unterprogramm) auf die Verarbeitung bestimmter Werte «eingestellt» werden kann. Parameter sind also programmextern gesetzte Einflussfaktoren; sie werden insbesondere beim Aufruf von Unterprogrammen verwendet, um diesen ‚mitzuteilen‘, welche Daten/Werte sie verarbeiten sollen und ggf. wie.
Durch Parametrisierung können Programme in ihrer Anwendung flexibilisiert werden, ohne dass das Programm dazu neu erstellt werden muss. Welche Werte eingestellt werden können, muss bei der Erstellung von Programmen festgelegt werden. Parameter können z. B. bestimmte Grenzwerte/Auswahlbedingungen (für Beträge, ein Datum oder ähnliches) oder zu verwendende Texte sein oder auch das «Was» und das «Wie» der Verarbeitung steuern (z. B. Prüfung X vornehmen – ja/nein).
Quelle: Wikipedia, Parameter (Informatik)
Auch der Begriff «Parameter» wird nicht in allen Fach- oder Anwendungsgebieten gleich verstanden – die obige Definition bezieht sich auf die allgemeine Verwendung des Begriffs in der Informatik (z.B. in Bezug auf Übergabewerte einer Methode). Im Kontext von Simulationen bezeichnen Parameter diejenigen Aspekte eines Modells, die bewusst flexibel angelegt wurden. Indem das Modell mit konkreten Werten für diese Parameter gefüttert wir, versetzt man es in eine bestimmte Situation oder einen bestimmten Zustand und simuliert dann das Verhalten.
Visualisierung
Mit Visualisierung oder Veranschaulichung (Sichtbarmachen) meint man im Allgemeinen, abstrakte Daten (z. B. Texte) und Zusammenhänge in eine grafische bzw. visuell erfassbare Form zu bringen. Im Speziellen bezeichnet Visualisierung den Prozess, sprachlich oder logisch nur schwer formulierbare Zusammenhänge in Grafiken, Tabellen und Schaubilder zu übersetzen, um sie verständlich zu machen. Weiterhin wird Visualisierung eingesetzt, um einen bestimmten Zusammenhang deutlich zu machen, der sich aus einem gegebenen Datenbestand ergibt, der aber nicht unmittelbar deutlich wird.
Dabei werden Details der Ausgangsdaten weggelassen, die im Kontext der gewünschten Aussage vernachlässigbar sind. Zudem sind stets gestalterische Entscheidungen zu treffen, welche visuelle Umsetzung geeignet ist und welcher Zusammenhang gegebenenfalls betont werden soll. Visualisierungen implizieren daher stets eine Interpretation der Ausgangsdaten, werden aber auch durch textliche oder sprachliche Angaben ergänzt, um eine bestimmte Interpretation zu kommunizieren.
Quelle: Wikipedia, Visualisierung
Rastergrafik vs. Vektorgrafik
Es gibt zwei grundsätzlich unterschiedliche Herangehensweisen für die binäre Repräsentation von Bildinformationen:
- Rastergrafiken, bei denen schlicht für jedes Pixel eine Farbe angegeben wird. Wichtige Merkmale einer Rastergrafik sind die Auflösung (also die Dimensionen des Rasters, ausgedrückt als Breite x Höhe) sowie die Codierung der Farbangaben (z.B. Farbraum und Farbtiefe).
- Vektorgrafiken, bei denen die grafischen Inhalte mithilfe geometrischer Formen (allgemeiner: Kurven bzw. Pfade) und zugehöriger Formeln beschrieben werden. Angegeben (meist als Text in einem XML-Format) wird jeweils die Art der Form (z.B. Kreis, Polygon oder Bezierkurve) und zugehörige Eigenschaften (z.B. Mittel-, End- oder Ankerpunkte, Farben, Strichbreiten), ggf. können auch Transformationseigenschaften und damit Animationen beschrieben werden.
Je nach Bildinhalt und Einsatzzweck eignet sich die eine oder die andere Herangehensweise. Rastergrafiken können einfach (pixelweise) verändert und dargestellt werden – beispielsweise wird einem typischen Bildschirm mindestens 60 Mal pro Sekunde (=60 Hz) für jedes einzelne Pixel die Information geschickt, welche Farbe es anzeigen soll. Ein Nachteil von Rastergrafiken liegt im hohen Speicherplatzbedarf. Zur Kompensation dieses Problem gibt es komprimierte Grafikformate (z.B. JPG, GIF oder PNG), die verschiedene Techniken anwenden, um die pixelbasierten Bildinformationen effizienter zu beschreiben, dabei aber einen gewissen Informationsverlust in Kauf nehmen.
Rastergrafiken sind einfach zu erstellen, z.B. mit einer Digitalkamera oder einem Scanner, aber sie sind immer an eine Auflösung (die Anzahl der Pixel) gekoppelt. Wenn das Bild über diese Auflösung hinaus vergrössert wird, fehlen die Informationen für die zusätzlichen Bildpunkte, also wird das Bild oder der Ausdruck unscharf bzw. verpixelt.
Hier spielt der grosse Vorteil von Vektorgrafiken: Weil die Inhalte als Formeln beschrieben sind, kann die pixelweise Darstellung (z.B. für Bildschirm oder Drucker) für beliebige Auflösungen ausgerechnet werden, das Bild bleibt immer scharf. Wichtig ist das unter anderem für Schriftarten: Wenn die Form der Buchstaben als Vektorgrafik gespeichert ist, kann dieselbe Datei für beliebige Schriftgrössen verwendet werden. Allerdings bieten sich Vektorgrafiken nur an, wenn sich die grafischen Inhalte für eine solche “geometrische” Beschreibung eignen. Zur Erstellung braucht man spezielle Vektorgrafikprogramme.
Vererbung
Beim ObjektOrientierten Programmieren (OOP) ist jede Klasse eine spezialisierte Version einer Oberklasse. Das bedeutet, dass ihr nicht nur die eigenen Eigenschaften (= Instanzvariablen) und Fähigkeiten (= Methoden) zur Verfügung stehen, sondern auch diejenigen all ihrer Oberklassen.
Auf diese Weise lässt sich Code effizient über verschiedene Ebenen einer Klassenhierarchie verteilen, weil allgemeiner, für mehrere Unterklassen geltender Code nur einmal (in der Oberklasse) definiert werden muss. So erspart man sich u.a. das aufwändige und fehleranfällige Kopieren von Code in verschiedene Klassen – und jede Klasse muss nur die Dinge definieren, die sie speziell machen.
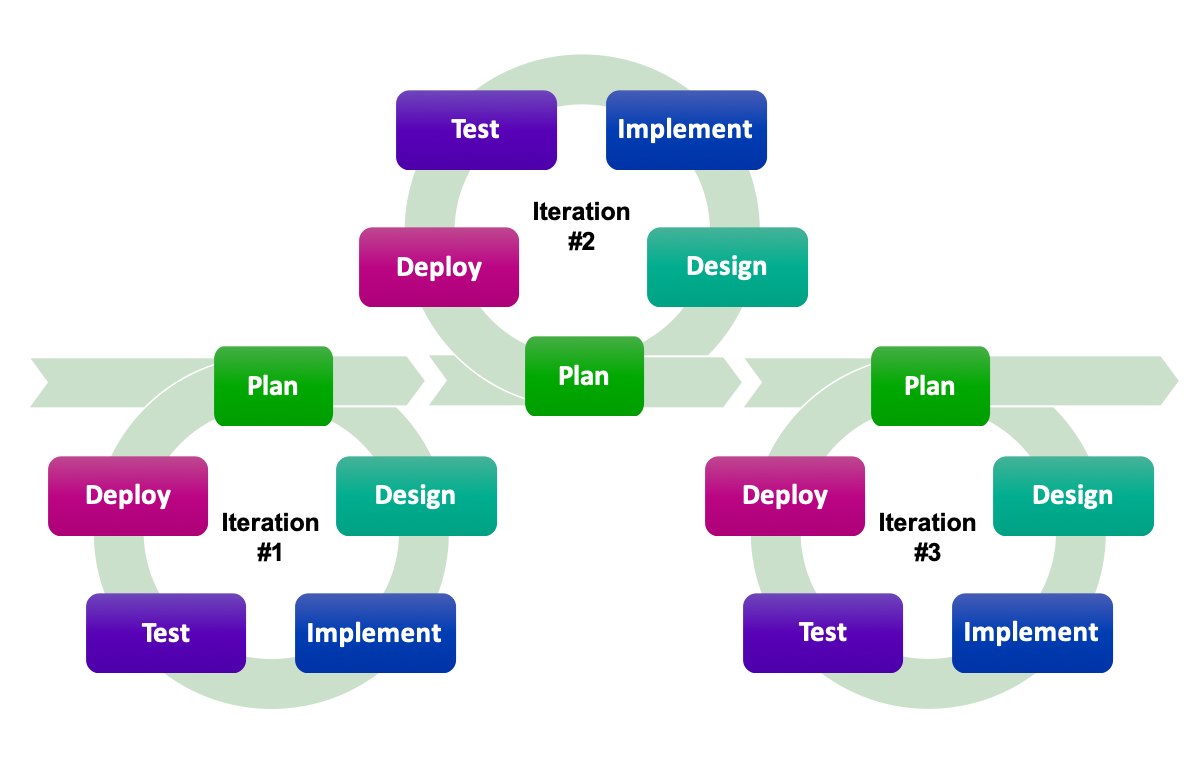
Iterative Development
Bei der iterativen Planung wird zu Beginn das Fernziel des Projekts nur grob festgelegt – die Planung und Entwicklung bezieht sich dann immer auf das Erreichen des jeweils nächsten Teilziels in Form einer neuen Version des Programms (oft «milestones» genannt), das der Idealvorstellung des Fernziels wieder ein Stückchen näher kommt. Innerhalb einer Iteration durch diesen «design cycle» finden sich dann die üblichen Schritte des Wasserfallmodells.
Gültigkeit vs. Sichtbarkeit
Gültigkeits-Bereich: Programmbereich, in dem die Variable existiert (d.h. einen Speicherplatz behält).
Sichtbarkeits-Bereich: Programmbereich, in welchem auf die Variable zugegriffen werden kann.
Kombinationen
Nicht nur am Computer ergibt sich immer wieder die Frage, wie viele verschiedene Kombinationsmöglichkeiten von Zeichen oder Ziffern sich für eine bestimmte Anzahl Stellen ergeben. Die Antwort ist immer dieselbe:
Möglichkeiten pro Stelle hoch Anzahl Stellen
Beispiele:
- Wenn ein Passwort aus 4 Kleinbuchstaben besteht, dann gibt es insgesamt 264 = 456976 verschiedene Passwörter (ein Hacker könnte diese Kombinationen mithilfe einer brute-force Attacke sehr schnell alle durchprobieren)
- Wenn die Farbe eines Pixels mit 3 Byte, also 24 Bit codiert ist, dann kann dieses Pixel 224 = ca. 16.7 Mio unterschiedliche Farben haben
- Wenn eine Dezimalzahl 3 Stellen lang ist, dann gibt es 103 = 1000 verschiedene Möglichkeiten. Weil die Null auch eine dieser Möglichkeiten ist, können wir mit drei Stellen von 0 bis 999 zählen
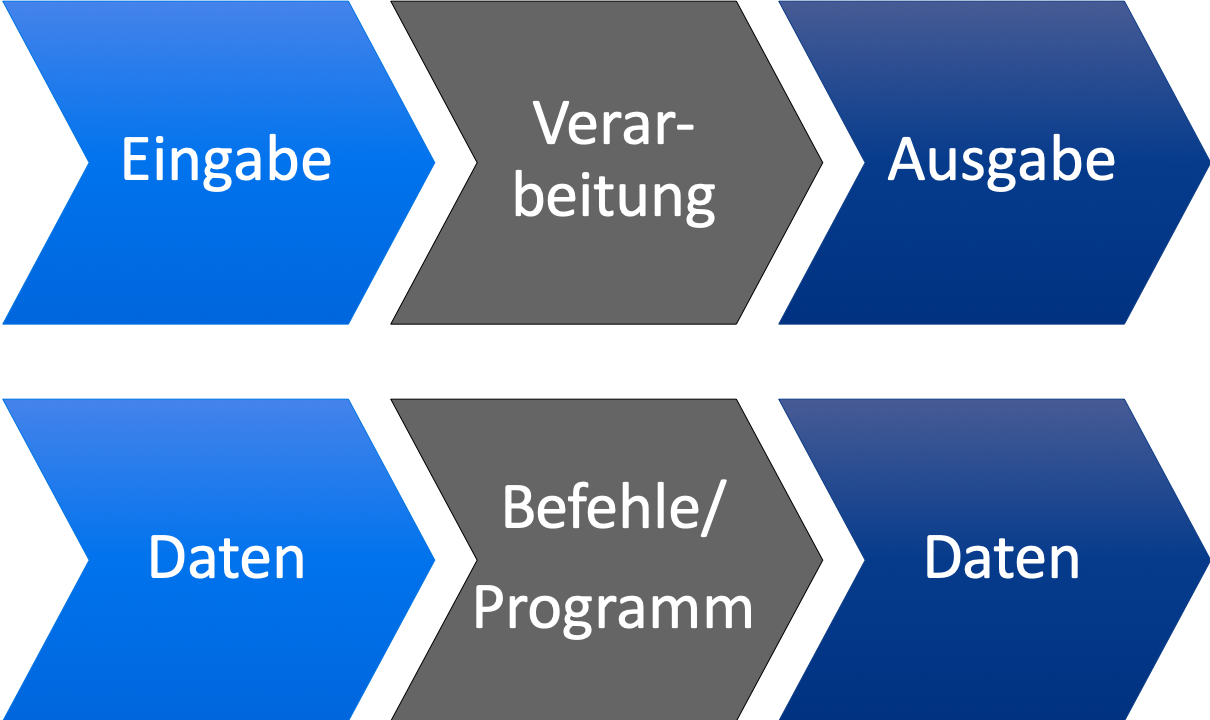
EVA
EVA: Eine Eingabe wird mittels automatischer Verarbeitung in eine Ausgabe verwandelt.
Beispiele:
- Sie schalten den Computer an (= Eingabe) – es dauert ein Weilchen, bis er gebootet hat (= Verarbeitung): Sie sehen die Oberfläche des Betriebssystems (= Ausgabe).
- Sie klicken auf das Firefox-Icon (das ist die Eingabe) – das Programm wird in den Arbeitsspeicher geladen (= Verarbeitung): Sie sehen das Browserfenster am Bildschirm (= Ausgabe).
- Sie schreiben www.oinf.ch in die Adressleiste des Browsers und drücken Return (E) – die Webseite wird aus dem Internet geholt und in einem temporären Cache lokal gespeichert (V): Die Seite wird im Browserfenster angezeigt (A).
- Sie tippen 5+17 in ein Rechenprogramm (E) – die Rechnung wird ausgeführt (V): Das Ergebnis 22 wird angezeigt oder abgespeichert (A).
- Sie schreiben
move();in die act-Methode einer Actor-Klasse im Greenfoot Editor und lassen das Szenario laufen (E) – der Code wird kompiliert und ausgeführt (V): Das Bild der Actor-Instanz bewegt sich um 10 Pixel geradeaus (A).
Digital vs. Analog
Nicht nur Zahlen werden am Computer im Binärsystem dargestellt, auch jegliche andere Informationen können digitalisiert werden. Analoge Informationen sind an ein physisches Medium gebunden, sie sind üblicherweise kontinuierlich; beispielsweise repräsentiert die Höhe der Quecksilbersäule in einem Thermometer die Temperatur ohne Abstufungen. Bei der Digitalisierung hingegen werden Informationen in diskrete Abstufungen (meist Zahlen) umgewandelt, die durch Bit (im Binärsystem) repräsentiert werden. Bei der Umwandlung in Zahlen muss die Genauigkeit immer vorgegeben sein, man muss auf eine vorher bestimmte Anzahl Stellen runden: Wenn man beispielsweise als Temperaturangabe Grad Celsius mit nur einer Nachkommastelle verwendet, dann wird zwischen 31.66 und 31.69 Grad nicht unterschieden.